Mean deviation for ungrouped data or Individual data with some examples
To find the mean deviation for ungrouped or individual data, we will follow these steps:
1. Collect the Data:
Let's consider the data set:
x={340,20,80,90,30,40,100,120}
2. Arrange the Data in Ascending Order:
We need to sort the data from smallest to largest:
x={20,30,40,80,90,100,120,340}
3. Determine the Number of Observations (n):
Count the total number of observations:
n=8
4. Calculate the Median:
Since n is even, the median is the average of the two middle numbers. The two middle numbers are the 4th and 5th numbers in the sorted list:
Median=80+902=1702=85
5. Calculate the Absolute Deviations:
Now, we will calculate the absolute deviations from the median (85):
|xi−Median|=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩|20−85|=65|30−85|=55|40−85|=45|80−85|=5|90−85|=5|100−85|=15|120−85|=35|340−85|=255
6. Sum of Absolute Deviations:
Add all the absolute deviations:
Sum=65+55+45+5+5+15+35+255=485
7. Calculate the Mean Deviation:
Finally, divide the sum of absolute deviations by the number of observations:
Mean Deviation=Sum of Absolute Deviationsn=4858=60.625
Final Result:
The mean deviation for the given data set is 60.625.
---
Let's consider the data set:
x={340,20,80,90,30,40,100,120}
We need to sort the data from smallest to largest:
x={20,30,40,80,90,100,120,340}
Count the total number of observations:
n=8
Since n is even, the median is the average of the two middle numbers. The two middle numbers are the 4th and 5th numbers in the sorted list:
Median=80+902=1702=85
Now, we will calculate the absolute deviations from the median (85):
|xi−Median|=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩|20−85|=65|30−85|=55|40−85|=45|80−85|=5|90−85|=5|100−85|=15|120−85|=35|340−85|=255
Add all the absolute deviations:
Sum=65+55+45+5+5+15+35+255=485
Finally, divide the sum of absolute deviations by the number of observations:
Mean Deviation=Sum of Absolute Deviationsn=4858=60.625
The mean deviation for the given data set is 60.625.
Similar Questions
Knowledge Check
The mean deviation of an ungrouped data is 10. If each observation is increased by 4% the revised mean deviations is
A10.0B10.4C10.04D9.6The mean deviation of an unground data is 50. If each observation is increased by 2% then the new mean deviation is
A50B21C49D50.5The mean deviation from the mean for the following data is
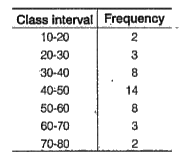 A5B10C15D20
A5B10C15D20
Raw data or ungrouped data.
View SolutionMEDIAN of an ungrouped data
View SolutionExercise-14.2 || Examples on Mode, Mean comparing || Median OF ungrouped data || Revise studied in 9th class
View SolutionThe mean deviation from the mean for the following data is
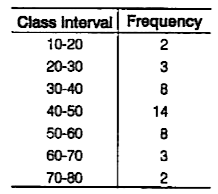
View SolutionFind the mean deviation about the mean for the following data :
Find the mean deviation about the mean for the following data :
7,8,4,13,9,5,16,18
View Solution
