Rational Number with examples
Rational Number with Examples
When it comes to rational numbers in Maths, they are represented in the form of p/q. Here, q is not equivalent to zero. In this case, non-zero denominators of any fraction is a rational number. Therefore, it can be said 0 is a rational number for the simple reasons that it can be represented in different forms like 0/1, 0/2, 0/3,0/4, etc. are not rational. Here, we will learn about irrational numbers as well. We will also find some idea about the properties of rational numbers. Addition of solved examples can help in understanding the concepts in the right manner.
Rational Number Definition
Any number which can be expressed in the form of p/q and is also greater than 0, then it is known as a rational number in Mathematics. Here, we will get the perfect knowledge on how to identify rational numbers.
Identifying a number is rational or not, it is important to check the conditions as below:
It should be in the form of p/q, where q≠0.
The ratio p/q can be further represented as well as simplified in the decimal form.
Examples of Rational Numbers:
p
q
p/q
Rational/Irrational Number
10
2
10/2 =5
Rational
1
1000
1/1000 = 0.001
Rational
50
10
50/10 = 5
Rational
7
0
Jul-00
Irrational (because q=0)
Types of Rational Numbers
If a number can be written in a fraction form, then it is rational. Here, both numerator and denominator are integers.
Standard Form of Rational Numbers
If there are no common factors except the one between the dividend and divisor, then the standard format of a rational number can be expressed. Thus, the divisor is positive. For example, we can say that 12/36 is a rational number
Positive and Negative Rational Numbers
Positive Rational Numbers
Negative Rational Numbers
Same signs for both the numerator and denominator.
Opposite signs for numerator and denominator.
All are found to be greater than 0
All are found to be less than 0
Example: 9/11, 12/17, and 3/5 are positive rational numbers
Example: 9/-11, -1/5, and -2/17, are negative rational number
Arithmetic Operations on Rational Numbers
In Maths, arithmetic operations happen to be the basic operations that are performed on integers. We will have a look as to how these operations on rational numbers can be performed, for example, p/q and s/t.
Addition: When p/q and s/t are added, it is important to make the denominator same. Here, we find (pt+qs)/qt.
For example: 1/2 + 3/4 = (2+3)/4 = 5/4
Subtraction: In the same way, if p/q and s/t are subtracted, then also, we have to make the denominator same, first, and then do the subtraction.
For example: 1/2 – 3/4 = (2-3)/4 = -1/4
Multiplication: Here, the numerator and denominators of the rational numbers are multiplied while multiplying two rational numbers. For example, when If p/q is multiplied by s/t, then we get (p×s)/(q×t).
For example: 1/2 × 3/4 = (1×3)/(2×4) = 3/8
Division: If p/q and s/t are divided, then it is represented as:
(p/q)÷(s/t) = pt/qs
For example: 1/2 ÷ 3/4 = (1×4)/(2×3) = 4/6 = 2/3
Related Videos:
- Irrational Number with examples
- Give examples of two irrational numbers the product of which is: (i) a rational number (ii) an irrational number
Rational Numbers Properties
- When one looks at the result of two rationals, it is always found to be a rational number when we add, multiply or subtract them.
- A rational number remains the same if we multiply or divide both the numerator and denominator with the same number.
Rational Numbers and Irrational Numbers
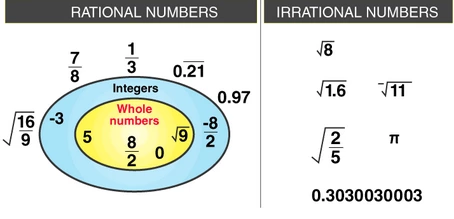
There are some differences between rational and irrational numbers. A rational number consists of a fraction with non-zero denominators is called a rational number. Number ½ is a rational number. The reason is simple due to the fact that it is read as integer 1 divided by the integer 2. Irrational numbers are those that are not rational.
Rationals can be positive, negative or zero. When it comes to specifying the negative rational number, the negative sign is either in front or with the numerator, which is the standard mathematical notation. For example, we denote negative of 7/2 as -57/2.
It is important to note that an irrational number cannot be written as a fraction. Instead, it can be written as a decimal. Some of the irrational numbers which are mentioned are:
π = 3.142857…
√2 = 1.414213…
Important Chapters:
p
q
p/q
Rational/Irrational Number
10
2
10/2 =5
Rational
1
1000
1/1000 = 0.001
Rational
50
10
50/10 = 5
Rational
7
0
Jul-00
Irrational (because q=0)
Positive Rational Numbers
Negative Rational Numbers
Same signs for both the numerator and denominator.
Opposite signs for numerator and denominator.
All are found to be greater than 0
All are found to be less than 0
Example: 9/11, 12/17, and 3/5 are positive rational numbers
Example: 9/-11, -1/5, and -2/17, are negative rational number
(p/q)÷(s/t) = pt/qs

Similar Questions
Basic Maths Number system ( Natural number || Complex number || Rational and Irrational number) and examples
View SolutionRational Numbers|Examples|OMR
View SolutionRational Numbers|Examples|OMR
View SolutionWhat are rational numbers? Give Examples of five positive and five negative rational numbers. Is there any rational number which is neither positive nor negative? Name it.
View SolutionTwin prime Number | | Prime Triplet||Finding Rational Number b\w Two number, Rational number in decimal Representation || Long- division method ||Nature OF the Decimal Expansion ||Example
View SolutionBetween any two rational numbers there are exactly ten rational numbers.
View SolutionGive an example of two irrational numbers whose sum as well as product is rational.
View SolutionGive an example of two irrational numbers whose sum is rational
View SolutionGive an example of two or more rational numbers whose denominators with no common factors.
View Solutiongive one example of two irrational number whose difference is a rational number and sum is irrational number .
View Solution
