Thales Theorem ( Basic Proportionality Theorem)
Step-by-Step Solution for Thales Theorem (Basic Proportionality Theorem)
Step 1: Understand the Theorem
Thales Theorem states that if a line is drawn parallel to one side of a triangle, it intersects the other two sides in such a way that the segments on those sides are proportional.
Step 2: Draw the Triangle
Let’s consider a triangle ABC. Draw a line parallel to side BC that intersects sides AB and AC at points D and E respectively.
Step 3: Identify the Ratios
We need to prove that:
ADDB=AEEC
Step 4: Construct Perpendiculars
From points D and E, draw perpendiculars to the opposite sides. Let the perpendicular from D to AC meet at point M and the perpendicular from E to AB meet at point N.
Step 5: Calculate Areas of Triangles
- The area of triangle ADE can be expressed as:
AreaADE=12×AD×EN
- The area of triangle BDE can be expressed as:
AreaBDE=12×BD×EN
- The area of triangle DEC can be expressed as:
AreaDEC=12×CE×DM
Step 6: Set Up Proportions
From the areas calculated:
1. For triangles ADE and BDE:
AreaADEAreaBDE=AD⋅ENBD⋅EN=ADBD
2. For triangles ADE and DEC:
AreaADEAreaDEC=AD⋅ENCE⋅DM=ADCE
Step 7: Use the Equal Areas of Triangles
Since triangles BDE and CED are between the same parallel lines, their areas are equal:
AreaBDE=AreaCED
Step 8: Final Proportions
Thus, we can equate the ratios:
ADBD=AEEC
Conclusion:
We have shown that:
ADDB=AEEC
This proves Thales Theorem.
---
Thales Theorem states that if a line is drawn parallel to one side of a triangle, it intersects the other two sides in such a way that the segments on those sides are proportional.
Let’s consider a triangle ABC. Draw a line parallel to side BC that intersects sides AB and AC at points D and E respectively.
We need to prove that:
ADDB=AEEC
From points D and E, draw perpendiculars to the opposite sides. Let the perpendicular from D to AC meet at point M and the perpendicular from E to AB meet at point N.
- The area of triangle ADE can be expressed as:
AreaADE=12×AD×EN
- The area of triangle BDE can be expressed as:
AreaBDE=12×BD×EN
- The area of triangle DEC can be expressed as:
AreaDEC=12×CE×DM
From the areas calculated:
1. For triangles ADE and BDE:
AreaADEAreaBDE=AD⋅ENBD⋅EN=ADBD
2. For triangles ADE and DEC:
AreaADEAreaDEC=AD⋅ENCE⋅DM=ADCE
Since triangles BDE and CED are between the same parallel lines, their areas are equal:
AreaBDE=AreaCED
Thus, we can equate the ratios:
ADBD=AEEC
We have shown that:
ADDB=AEEC
This proves Thales Theorem.
Similar Questions
Knowledge Check
Thales theorem is given by a greek mathematician. According to this theorem, if a line is drawn parallel to one side of a triangle then it divides the other two sides in the same ratio. This theorem is also known as Basic Proportionality Theorem.
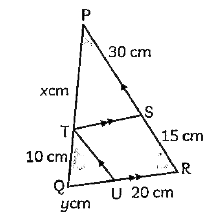
Here, the value of x is :A20 cmB15 cmC5 cmD10 cm
Basic Proportionality Theorem|Converse Of BPT (Basic Proportionality Theorem) (Thales Theorem)|NCERT Example Questions
View SolutionBasic Proportionality Theorem (Thale's Theorem)|Converse Of Basic Proportionality Theorem|Example|Questions|OMR
View SolutionTriangles|Basic Proportionality Theorem(BPL)Thales Theorem|Converse Of (Basic Proportionality Theorem(BPL))Thales Theorem|Criteria For Similarity Of Triangles |Pythagoras Theorem And Its Converse
View SolutionCongruent Triangles|Criteria For Congruence Of Triangles|Questions|Basic Proportionality Theorem (Thale's Theorem)|Quiz|OMR
View SolutionExercise Questions|Basic Proportionality Theorem
View SolutionState the basic proportionality theorem.
View SolutionOMR|Converse Of Basic Proportionality Theorem|Questions|Criteria For Similarity Of Triangles|Theorem|Questions|Theorem
View Solution
