Let, X denote the number of colleges where you will apply after your results and P (X = x) denotes your probability of getting admission in x number of colleges. It is given that P(X=x)={kx,ifx=0or12kx,ifx=2k(5−x),ifx=3or40,ifx>4 where k is a positive constant. Find the value of k . Also find the probability that you will get admission in (i) exactly one college (ii) at most 2 colleges (iii) at least 2 colleges.
To solve the problem, we need to find the value of k and the required probabilities based on the given probability mass function P(X=x).
Step 1: Determine the value of k
The probability mass function is given as:
- P(X=x)=kx for x=0 or 1
- P(X=x)=2k for x=2
- P(X=x)=k(5−x) for x=3 or 4
- P(X=x)=0 for x>4
We need to ensure that the sum of all probabilities equals 1:
P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)=1
Calculating each probability:
- P(X=0)=k⋅0=0
- P(X=1)=k⋅1=k
- P(X=2)=2k
- P(X=3)=k(5−3)=2k
- P(X=4)=k(5−4)=k
Now, summing these probabilities:
0+k+2k+2k+k=6k
Setting the sum equal to 1:
6k=1⟹k=16
Step 2: Find the probability of getting admission in exactly one college
Using the value of k:
P(X=1)=k=16
Step 3: Find the probability of getting admission in at most 2 colleges
This includes the probabilities for X=0, X=1, and X=2:
P(X=0)+P(X=1)+P(X=2)=0+k+2k=0+16+2⋅16=0+16+26=36=12
Step 4: Find the probability of getting admission in at least 2 colleges
This includes the probabilities for X=2, X=3, and X=4:
P(X=2)+P(X=3)+P(X=4)=2k+2k+k=2⋅16+2⋅16+16=26+26+16=56
Summary of Results
1. The value of k is 16.
2. The probability of getting admission in exactly one college is 16.
3. The probability of getting admission in at most 2 colleges is 12.
4. The probability of getting admission in at least 2 colleges is 56.
- P(X=x)=kx for x=0 or 1
- P(X=x)=2k for x=2
- P(X=x)=k(5−x) for x=3 or 4
- P(X=x)=0 for x>4
P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)=1
- P(X=0)=k⋅0=0
- P(X=1)=k⋅1=k
- P(X=2)=2k
- P(X=3)=k(5−3)=2k
- P(X=4)=k(5−4)=k
0+k+2k+2k+k=6k
6k=1⟹k=16
P(X=1)=k=16
P(X=0)+P(X=1)+P(X=2)=0+k+2k=0+16+2⋅16=0+16+26=36=12
P(X=2)+P(X=3)+P(X=4)=2k+2k+k=2⋅16+2⋅16+16=26+26+16=56
2. The probability of getting admission in exactly one college is 16.
3. The probability of getting admission in at most 2 colleges is 12.
4. The probability of getting admission in at least 2 colleges is 56.
Topper's Solved these Questions
Similar Questions
Let 'X' denote the number of hours you study during a randomly selected school day. The probability that 'X' can take the values of x has the following form, where k is some unknown constant.
P(X=x)={(0.1,,if,x=0),(kx,,if,x=1 or 2),(k(5−x),,if,x=3 or 4),(0,,,otherwise.
(a) Find the value of 'k'.
(b) What is the probability that you study at least two hours ? Exactly two hours ? At most two hours ?
View SolutionLet X denote the number of hours you study during a randomly selected school day The probability that X can take the values x. has the following form, where k is some unknown constant.P(X=x)={0. 1 if x=0,k x if x=1 , 2k(5-x) if x=3 or 4, 0 otherwise
View Solution
Knowledge Check
Let denote the number of fruits that are grown in a farm house in a particular day. The probability that X can take the value of x has the following form, where k is some unknown constant.
P(X=x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩kifx=02kifx=13xifx=20otherwise
Then the value of k isA18B12C13D16If -2 is a root of the equation 3x2+7x+p=0, find the value of k so that the roots of the equation x2+k(4x+k−1)+p=0 are equal.
A−2,32B−1,23C−5,45D−3,75
The probability distribution of a random variable X is given as under: P(X=x)={kx2forx=1,2,32kxforx=4,5,60otherwise , where k is a constant. Find (i) P(X≥4 ) (ii) E(X) (iii) E(3X2)
View SolutionLet X denote the number of hours you study during a randomly selected school day. The probability that X take the values of x has the following form, where k is some unknown constant. P(X=x)={(0.1ifx=0),(kx,ifx=1or2),(k(5−x),ifx=3or4),(0,otherwise)
Find:
(i) k
(ii) the probability that you study exactly two hours,
(iii) the probability that you study at most two hours.
View SolutionFind the value of k if x+1 is a factor of p(x): p(x)=kx2+3x+k
View SolutionThe random variable X has a probability distribution P(X) of the following form, where k is some number :P(X) = {(k,ifx=0),(2k,ifx=1),(3k,ifx=2),(0otherwise)(a) Determine k.(b) Find P (X<2) , P (X≤2) , P(X≥2)
View SolutionThe probability distribution of X is as follows:
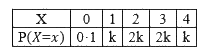
Find k and P [X<2].
View SolutionFind the value of k, if x−1is a factor of 4x3+3x2−4x+k.
View Solution
