In the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
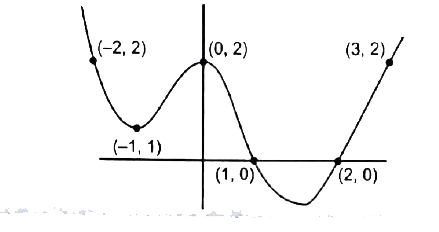
The minimum number of real roots of equation (p'(x))2+p(x)p''(x)=0 are:
3
4
5
6
The correct Answer is:B
Step by step video & image solution for In the given figure graph of : y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ …..+ a _(n) is given. The minimum number of real roots of equation (p' (x))^(2) +p(x)p''(x) =0 are: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATION OF DERIVATIVES BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (MATHCING TYPE PROBLEMS)
1 Videos
- APPLICATION OF DERIVATIVES BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
22 Videos
- APPLICATION OF DERIVATIVES BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (ONE OR MORE THAN ANSWER IS/ARE CORRECT )
29 Videos
- AREA UNDER CURVESBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - AREA UNDER CURVESEXERCISE - AXERCISE (SUBJECTIVE TYPE PROBLEMS)
8 Videos
Similar Questions
In the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
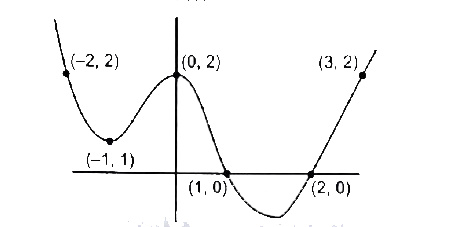
The product of all imaginary roots of p(x)=0 is:
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
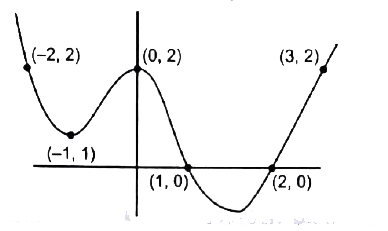
If p(x)+k=0 has 4 distinct real roots α,β,γ,δ then[α]+[β]+[γ]+[δ], (where [.] denotes greatest integer function) is equal to:
View Solution
Knowledge Check
If (1+x+x2+x3)n=a0+a1x+a2x2+………..a3nx3n then which of following are correct
Aa0+a1+a2+……+a3n=22nBa0+a2+a4+……=a1+a3+a5+……..Ca0=a3n,a1=a3n−1,a2=a3n−2Da0+a2+a4+…….=22n−1The number of real roots of he equation 1+a1x+a2x2+………..+anxn=0 where |x|<13 and |an|<2 is
An if n is evenB0 for any natural number nC1 if n is oddDNone of these
Differentiate |x|+a0xn+a1xn−1+a2xn−1+...+an−1x+an
View SolutionDifferentiate the following with respect of x:a0xn+a1xn−1+a2xn−2++an−1x+an.
View Solution(1+x)n=a0+a1x+a2⋅x2+.........+anxn then prove that
View SolutionIf the roots of the given equation (cosp−1)x2+(cosp)x+sinp=0 are real if
View Solutiona0fn(x)+a1fn−1(x).g(x)+a2fn−2g2(x)+......+angn(x)≥0
View SolutionLet f(x)=a0xn+a1xn−1+a2xn−2+.......+an,(a0≠0) if a0+a1+a+2+......+an=0 then the root of f(x) is
View Solution
