In a triangle AOB, R and Q are the points on the side OB and AB respectively such that 3OR = 2RB and 2AQ = 3QB. Let OQ and AR intersect at the point P (where O is origin).
Q. If the point P divides OQ in the ratio of μ:1, then μ is :
219
217
215
109
The correct Answer is:D
Topper's Solved these Questions
- VECTOR & 3DIMENSIONAL GEOMETRYBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-4 : Matching Type Problems
1 Videos
- VECTOR & 3DIMENSIONAL GEOMETRYBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-5 : Subjective Type Problems
18 Videos
- VECTOR & 3DIMENSIONAL GEOMETRYBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-2 : One or More than One Answer is/are Correct
21 Videos
- TRIGONOMETRIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems
9 Videos
Similar Questions
Consider a triangle ABC. The sides AB and AC are extended to points D and E respectively, such that AD=3ABandAE=3AC. Then one diagonal of BDEC divides the other diagonal in the ratio p:q then p+q=
View SolutionIn a triangle OAB, ∠AOB=900. If P and Q are points of trisection of AB prove that OP2+OQ2=59AB2.
View Solution
Knowledge Check
In a triangle AOB, R and Q are the points on the side OB and AB respectively such that 3OR = 2RB and 2AQ = 3QB. Let OQ and AR intersect at the point P (where O is origin).
Q. If the ratio of area of quadrilateral PQBR and area of ΔOPA is αβ then (β−α) is (where αandβ are coprime numbers) :A1B9C7D0In a triangle AOB, R and Q are the points on the side OB and AB respectively such that 3OR = 2RB and 2AQ = 3QB. Let OQ and AR intersect at the point P (where O is origin).
Q. If the ratio of area of quadrilateral PQBR and area of ΔOPA is αβ then (β−α) is (where αandβ are coprime numbers) :A1B9C7D0D and E are the mid-points of the sides AB and AC of ΔABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is
Aa squareBa rectangleCa rhombusDa parallelogram
In a triangle OAB,∠AOB=900. If P and Q are points of trisection of AB, prove that OP2+OQ2=59AB2
View SolutionIn a right triangle ABC , right angled at C, P and Q are the points of the sides CA and CB respectively , which divide these sides in the ratio 2:1 Prove that
9(AQ2+BP2)=13AB2
View SolutionA transversal cuts side AB and AD and diagonal AC of parallelogram ABCD in points P,Q and R respectively such that AP: PB =1 :2 and AQ: QD=2:3 . Find the ratio AR : RC
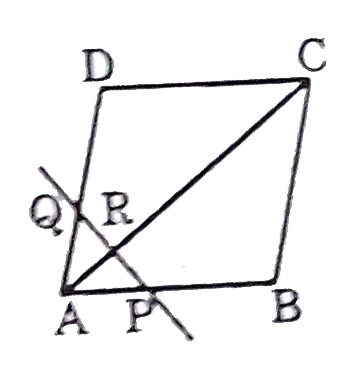
View SolutionIf O is the origin and Q is a variable point on y2=x. Find the locus of the mid point of OQ.
View SolutionA transversal cuts side AB and AD and diagonal AC of parallelogram ABCD in points P,Q and R respectively such that AP: PB =1 :2 and AQ: QD=2:3 . Find the ratio AR : RC

View Solution
