Question

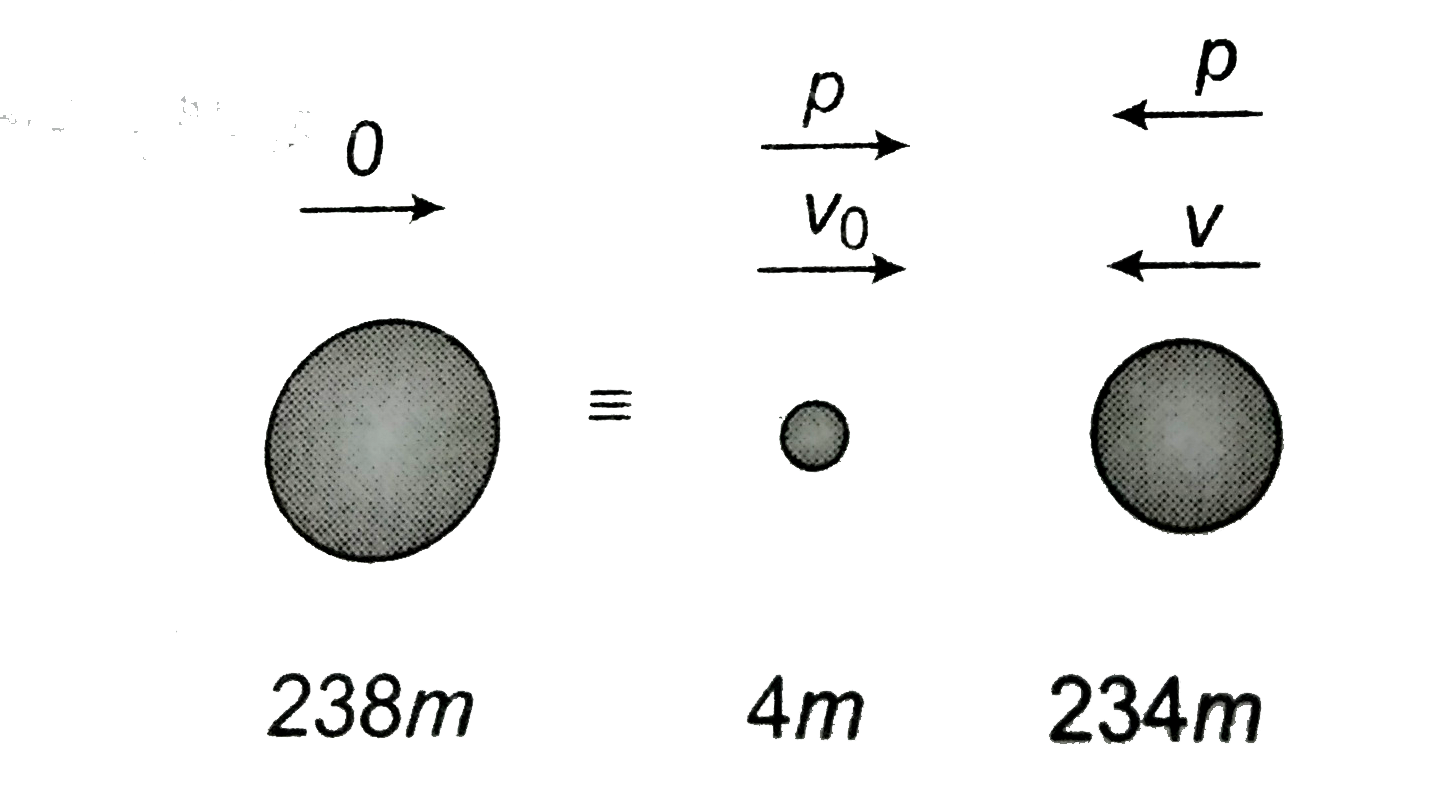
A $U^{238}$ nucleus , initially at rests , emits an alpha particle with a speed $v_0$. Calculate the recoil speed of the residual nucleus $T{h}^{234}$. Assume that the mass of a nucleus is proportional to the mass number. Also , calculate the ratio of $K.E.ofT{h}^{234}$ and $\alpha$ -particle.

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the Problem
We have a Uranium-238 nucleus that is initially at rest and emits an alpha particle. We need to find the recoil speed of the residual Thorium-234 nucleus and the ratio of their kinetic energies.

Step 2: Define the Masses
- Mass of Uranium-238 nucleus \( (U^{238}) \) = \( 238M \)
- Mass of alpha particle \( (He^{4}) \) = \( 4M \)
- Mass of Thorium-234 nucleus \( (Th^{234}) \) = \( 234M \)

Step 3: Apply Conservation of Momentum
Since the initial momentum of the system is zero (the Uranium nucleus is at rest), the final momentum must also equal zero.

Let:
- \( v_0 \) = speed of the emitted alpha particle
- \( v \) = recoil speed of the Thorium-234 nucleus

Using conservation of momentum:
\( \text{Initial Momentum} = \text{Final Momentum} \)
\( 0 = (4M)(v_0) + (234M)(-v) \)
This can be simplified to:
\( 0 = 4Mv_0 - 234Mv \)

Step 4: Solve for Recoil Speed \( v \)
Rearranging the equation gives:
\( 234Mv = 4Mv_0 \)
Dividing both sides by \( M \) (mass cancels out):
\( 234v = 4v_0 \)
Now, solving for \( v \):
\( v = \frac{4v_0}{234} = \frac{2v_0}{117} \)

Step 5: Calculate the Kinetic Energies
The kinetic energy (K.E.) of an object is given by the formula:
\( K.E. = \frac{1}{2}mv^2 \)

Kinetic Energy of the Alpha Particle:
\( K.E._{alpha} = \frac{1}{2}(4M)(v_0^2) = 2Mv_0^2 \)

Kinetic Energy of the Thorium-234 Nucleus:
\( K.E._{Th} = \frac{1}{2}(234M)\left(\frac{2v_0}{117}\right)^2 \)
Calculating this gives:
\( K.E._{Th} = \frac{1}{2}(234M)\left(\frac{4v_0^2}{13689}\right) = \frac{234 \cdot 2M v_0^2}{13689} = \frac{468Mv_0^2}{13689} \)

Step 6: Calculate the Ratio of Kinetic Energies
Now we can find the ratio of the kinetic energy of Thorium-234 to that of the alpha particle:
\( \text{Ratio} = \frac{K.E._{Th}}{K.E._{alpha}} = \frac{\frac{468Mv_0^2}{13689}}{2Mv_0^2} \)
Cancelling \( Mv_0^2 \) from the numerator and denominator gives:
\( \text{Ratio} = \frac{468}{2 \cdot 13689} = \frac{468}{27378} \)
Simplifying this ratio:
\( \text{Ratio} = \frac{1}{58.5} \)

Final Answers
1. The recoil speed of the Thorium-234 nucleus is \( v = \frac{2v_0}{117} \).
2. The ratio of the kinetic energy of Thorium-234 to that of the alpha particle is \( \frac{1}{58.5} \).