A particle of mass m experienced an elastic collision with a stationary particle of mass 2m . What fraction of the kinetic energy does the striking particle lose if recoils at the right angles to its original motion direction.
Since the total momentum before the collision is along the x-axis , the total momentum after the collision should be along the x-axis, for this particle of mass 2m should make at angle so that the net momentum along the y-axis is zero.
Fractional loss of K.E. of striking particle is
12mu2−12mv2112mu2=1−(v1u)2
By the momentum conservation:
Along the x-axis:
μ=2mv2cosθ⇒v2cosθ=u2 (i)
Along the y-axis:
0=mv1−2mv2sinθ⇒v2sinθ=v12 (ii)
Eliminating θ from (i) and (ii) , we get
(v2cosθ)2+(v2sinθ)2=u2+v214
v22=u2+v214
Since the collision is elastic
Ki=Kf
12mu2=12mv21+12×2mv22
u2=v21+2v22=v21+2(u2+v214)⇒(v1u)2=13
Fractional loss =1−(v1u)2=1−(13)=23
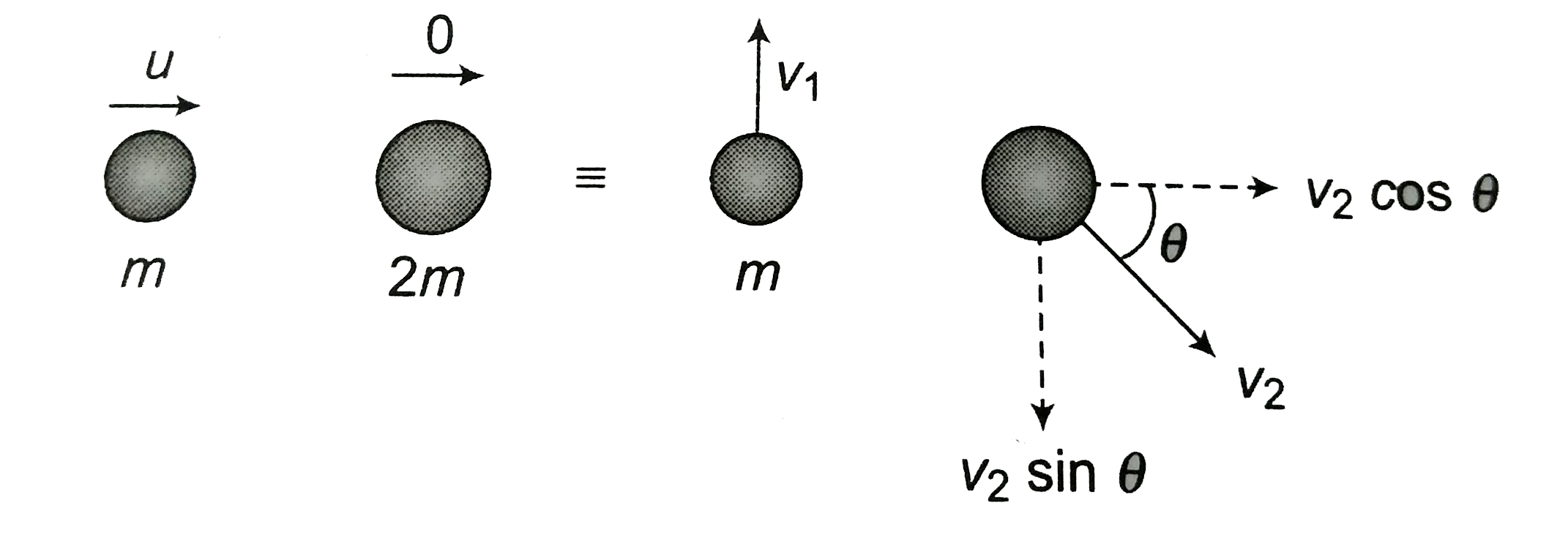
Topper's Solved these Questions
Similar Questions
A particle of mass m1 experienced a perfectly elastic collision with a stationary particle of mass m2. What fraction of the kinetic energy does the striking particle lose, if
(a) it recoils at right angles to its original motion direction,
(b) the collision is a head-on one?
View SolutionA particle of mass m moving with velocity v makes head-on elastic collision with a sationary particle of mass 2m. Kinetic energy lost by the lighter particle during period of deformation is
View Solution
Knowledge Check
A particle of mass m1 makes an elastic, one-dimensional collision with a stationary particle of mass m2.What fraction of the kinetic energy of m1 is carried away by m2?
Am1m2Bm2m1C2m1m2(m1+m2)2D4m1m2(m1+m2)2A particle of mass m1 makes an elastic one dimensional collision with a stationary particle of mass m2.What fraction of the kinetic energy of m1 is carried away by m2?
Am1m2Bm2m1C2m1m2(m1+m2)2D4m1m2(m1+m2)2A particle (A) of mass m1 elastically collides with another stationary particle (B) of mass m2. Then :
Am1m2=12 and the particles fly a part in the opposite direction with equal velocities.Bm1m2=13 and the particles fly apart in the opposite direction with equal velocities.Cm1m2=21 and the collision angle between the particles is 60∘ symmetrically.Dm1m2=21 and the particles fly apart symmetrically at an angle 90∘
A particle of mass m1 collides elastically with a stationary particle of mass m2(m1>m2). Find the maximum angle through which the striking particle may deviate as a result of the collision.
View SolutionA moving particle of mass 'm' makes head-on elastic collision with a particle of mass '2m' which is initially at rest.The fraction of K.E.lost by colliding particle is
View SolutionA ball of mass m1 makes an elastic , one-dimensional collision with a stationary particle of mass m2. The fraction of the kinetic energy of m1 transferred to m2 is
View SolutionA particle of mass m moving with velocity v makes head-on elastic collision with a sationary particle of mass 2m. Kinetic energy lost by the lighter particle during period of deformation is
View SolutionA particle of mass m moving with kinetic energy K, makes a head - on elastic collision with a stationary particle of mass ηm. The maximum potential energy stored in the system during the collision is
View Solution
