Two particles A and B of masses 2m and m are placed on a smooth surface at separation d. They move towards each other due to the mutual attractive force.
(i) The particles will meet at distance d/3 from the initial position of mass 2m.
(ii) The speed of A will be half of speed of B until the particles collide (excluding the initial speed).
(iii) The distance covered by B is always double that covered by A until the particles collide.
(iv) The velocity of center of mass is always zero.
(i),(ii)
(i),(ii),(iii)
(ii),(iii),(iv)
all options are correct
The correct Answer is:D
(i) Since the location of center of mass is fixed
2mx=m(d−x)⇒x=d3
(ii) Since the initial momentum of system is zero and it will always remain zero (since no external force)
0=2mvA−mvB⇒vA=vB2
(iii) 2mx1=mx2⇒vA=vB2
(iii) 2mx1=mx2⇒x2=2x1
(iv) →vc.m.=0= constant
Topper's Solved these Questions
Similar Questions
Two particles of masses 2m and 3m are placed at separation d on a smooth surface. They move towards each other due to mutual attractive force. Find (a) acceleration of c.m. (b) Velocity of c.m. when separation between particles becomes d/3. ( c) At what distance from the initial position of mass 2m, the particles collide.
View SolutionTwo charged particles of masses m and 2m are placed distane d apart on a smooth horizontal table. Because of their mutual attraction, they move towards each other and collide. Where will the collision occure with respect to the initial positions?
View Solution
Knowledge Check
Two particles of masses 4kg and 6kgareseparatedbyadistanceof20cm and are moving towards each other under mutual force of attraction, the position of the point where they meet is
A12mfrom 4kg bodyB12m from 6kg bodyC8m from 4kg bodyD10m from 4kg bodyTwo particles of mass M and 2M are at a distance D apart. Under their mutual force of attraction they start moving towards each other. The acceleration of their centre of mass when they are D/2 apart is :
A2GM/D2B4GM/D2C8GM/D2DZeroTwo particles of different masses initially at rest, start moving towards each other under their mutual gravitational attraction. At an instant when the speeds of the particles are v and 2v, the speed of the
AzeroBvC1.5 vD3 v
Two particles of masses m and M are initially at rest at an infinite distance part. They move towards each other and gain speeds due to gravitational attracton. Find their speeds when the separation between the masses becomes equal to d.
View SolutionConsider a system of two particles of masses m1 and m2 separated by a distance r. Suppose they start to move towards each other due to their mutual attraction (attractive force may be electrical, gravitational, etc.).
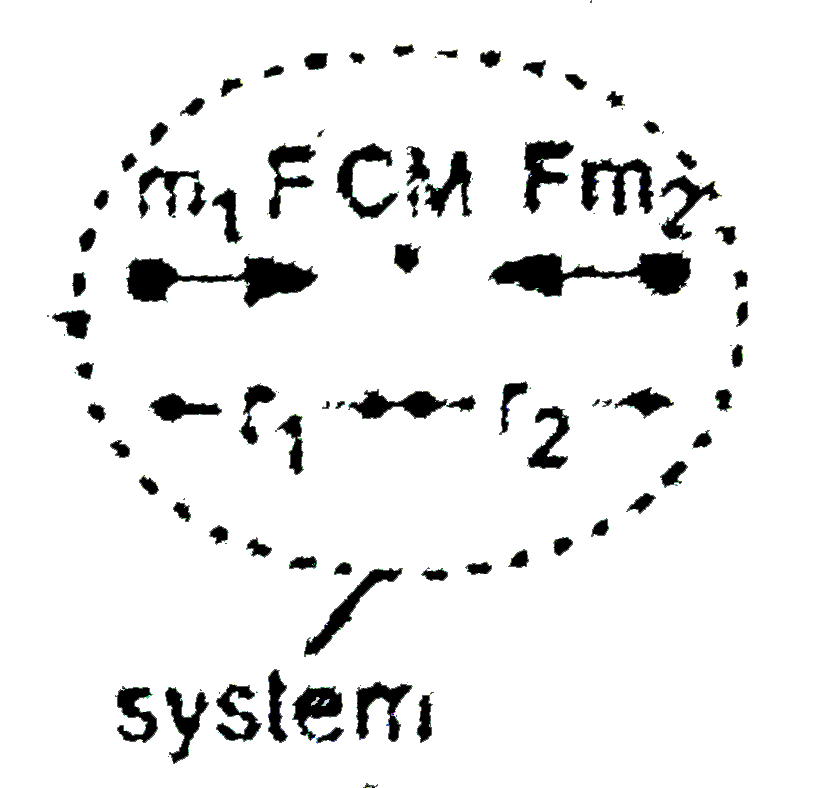
View Solution10 Two particles of masses m1 and m2 initially at rest start moving towards each other under their mutual force of attraction. The speed of the centre of mass at any time t, when they are at a distance r apart, is
View SolutionTwo particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then

View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
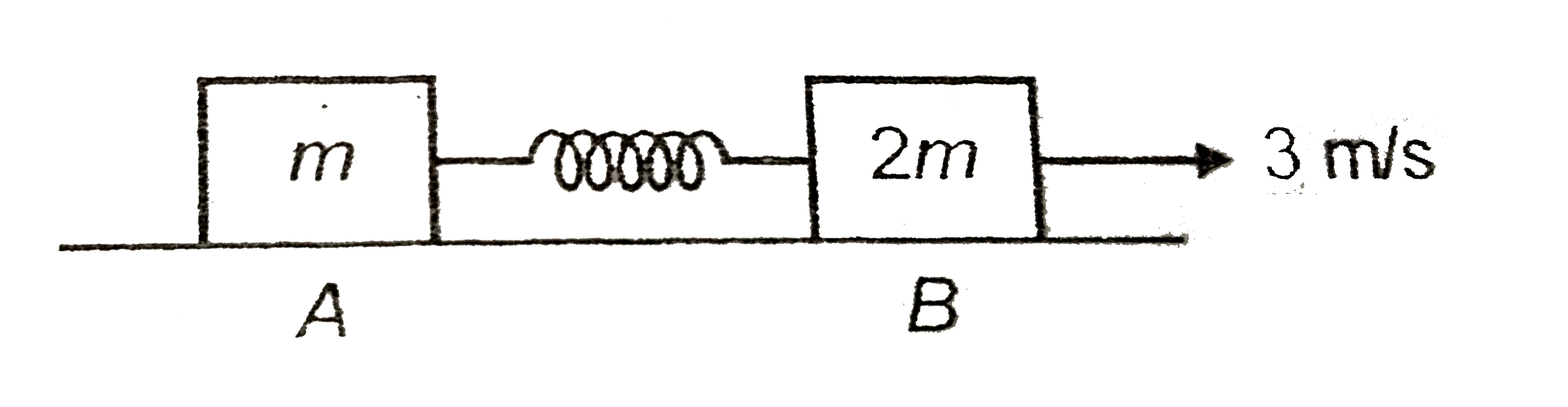
View Solution