An object , initially at rest , explodes in three fragments. The momentum of two pieces are $- 3 p ˆ i$ and $- 4 p ˆ j$ where $p$ is a positive number. The momentum of the third piece
(i) will have magnitude $5 p$
(ii) will make an angle ${tan}^{- 1} (4 / 3)$ with the $x$ -axis
(iii) will make an angle ${tan}^{- 1} (3 / 4)$ with the $x$ -axis
(iv) will have magnitude $7 p$

$(i), (i i i)$

$(i), (i i)$

$(i i), (i v)$

$(i i i), (i v)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let the momentum of the third piece be $p_{x} ˆ i + p_{y} ˆ j$ . By the momentum conservation
$0 = - 3 p ˆ i - 4 p ˆ j + p_{x} ˆ i + p_{y} ˆ j$
$= (- 3 p + p_{x}) ˆ i + (- 4 p + p_{y}) ˆ j$
$- 3 p + p_{x} = 0 \Rightarrow p_{x} = 3 p$
$- 4 p + p_{y} = 0 \Rightarrow p_{y} = 4 p$
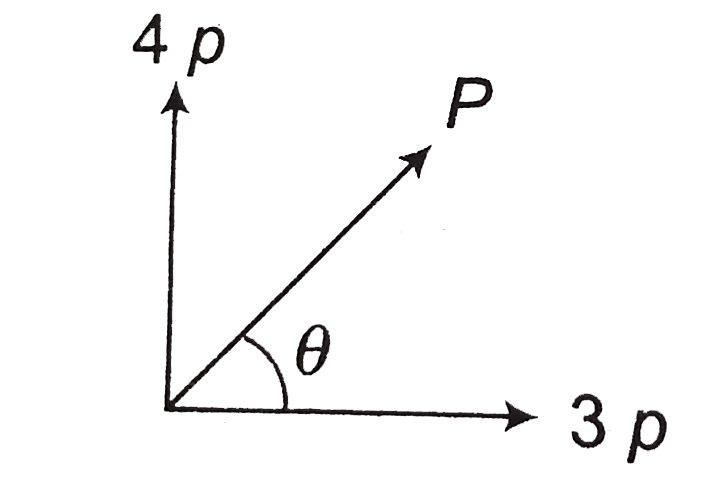
The momentum of third piece
$| \to p | = \sqrt{{(3 p)}^{2} + {(4 p)}^{2}} = 5 p$
$tan θ = \frac{4 p}{3 p} \Rightarrow θ = {tan}^{- 1} (\frac{4}{3})$

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
An object , initially at rest , explodes into three fragments of equal mass . The momenta of two parts are $2 p ˆ i and p ˆ j$ where p is a positive number . The momentum of the third part is
AWill be of the magnitude 3p inclined at ${tan}^{- 1} (\frac{1}{2})$ with x - axis
BWill be of the magnitude $\sqrt{5} p$ inclined at ${tan}^{- 1} (2)$ with x - axis
CWill be of the magnitude 3p inclined at $π - {tan}^{- 1} (\frac{1}{2})$ with x - axis
DWill be of the magnitude $\sqrt{5} p$ inclined at $π + {tan}^{- 1} (\frac{1}{2})$ with x - axis
Question 2 - Select One
An object initially at rest explodes into three fragments $A, B$ and $C$ .The momentum of $A$ is $p ˆ i$ and that of $B$ is $\sqrt{3} p ˆ j$
where $p$ is $a + v e$ number. The momentum of $C$ will be
A $(1 + \sqrt{3}) P$ in a direction making $120^{\circ}$ with A
B2P in a direction making $150^{\circ}$ with A
C2P in a direction making $150^{\circ}$ with B
D $(1 + \sqrt{3}) P$ in a direction making $150^{\circ}$ with B
Question 3 - Select One
An object initially at rest explodes into three fragments $A, B$ and $C$ . The momentum of $A$ is $p ˆ i$ and that of $B$ is $\sqrt{3} p ˆ j$
where $p$ is $a + v e$ number. The momentum of $C$ will be
A $(1 + \sqrt{3}) p$ in a direction making angle $120^{\circ}$ with that of $A$
B $(1 + \sqrt{3}) p$ in a direction making angle $150^{\circ}$ with that of $B$
C $2 p$ in as direction making angle $150^{\circ}$ with that $A$
D $2 p$ in a direction making angle $150^{\circ}$ with that of $B$ .

CP SINGH-CENTER OF MASS-Exercises

Home
Ask Doubt
Profile

The correct Answer is:B

Let the momentum of the third piece be pxˆi+pyˆj. By the momentum conservation 0=−3pˆi−4pˆj+pxˆi+pyˆj =(−3p+px)ˆi+(−4p+py)ˆj −3p+px=0⇒px=3p −4p+py=0⇒py=4p The momentum of third piece |→p|=√(3p)2+(4p)2=5p tanθ=4p3p⇒θ=tan−1(43)

Topper's Solved these Questions

Similar Questions

Knowledge Check

An object , initially at rest , explodes into three fragments of equal mass . The momenta of two parts are 2pˆiandpˆj where p is a positive number . The momentum of the third part is

An object initially at rest explodes into three fragments A,B and C.The momentum of A is pˆi and that of B is √3pˆj where p is a+ve number. The momentum of C will be

An object initially at rest explodes into three fragments A,B and C. The momentum of A is pˆi and that of B is √3pˆj where p is a+ve number. The momentum of C will be

CP SINGH-CENTER OF MASS-Exercises

An object , initially at rest , explodes into three fragments of equal mass . The momenta of two parts are $2 p ˆ i and p ˆ j$ where p is a positive number . The momentum of the third part is

An object initially at rest explodes into three fragments $A, B$ and $C$ .The momentum of $A$ is $p ˆ i$ and that of $B$ is $\sqrt{3} p ˆ j$
where $p$ is $a + v e$ number. The momentum of $C$ will be

An object initially at rest explodes into three fragments $A, B$ and $C$ . The momentum of $A$ is $p ˆ i$ and that of $B$ is $\sqrt{3} p ˆ j$
where $p$ is $a + v e$ number. The momentum of $C$ will be