In the previous problem , if the collision is inelastic and $e = 1 / 2$

A

After collision , the ball moves with $5 \sqrt{13} m / s$ at angle ${tan}^{- 1} (2 \sqrt{3})$ with horizontal

B

Force by wall on the ball is $375 N$ to right

C

Change in momentum of ball is $0.75 k g m / s$

D

All options are correct

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

In this case , the velocity component , perpendicular to the wall becomes $e$ times and reverses its direction
$v' = \sqrt{{(10 \sqrt{3})}^{2} + {(5)}^{2}} = \sqrt{325} = 5 \sqrt{13} m / s$
$tan α = \frac{10 \sqrt{3}}{5} = 2 \sqrt{3} \Rightarrow α = {tan}^{- 1} (2 \sqrt{3})$
$Δ p_{x} = m e v {cos 60}^{\circ} - (- v {cos 60}^{\circ})]$
$= m v {cos 60}^{\circ} (1 + e)$
$= 50 \times 10^{- 3} \times 20 \times \frac{1}{2} (1 + \frac{1}{2}) = 0.75 k g m / s$
$F_{x} = \frac{Δ p_{x}}{Δ t} = \frac{0.75}{2 \times 10^{- 3}} = 375 N$ , to the right

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

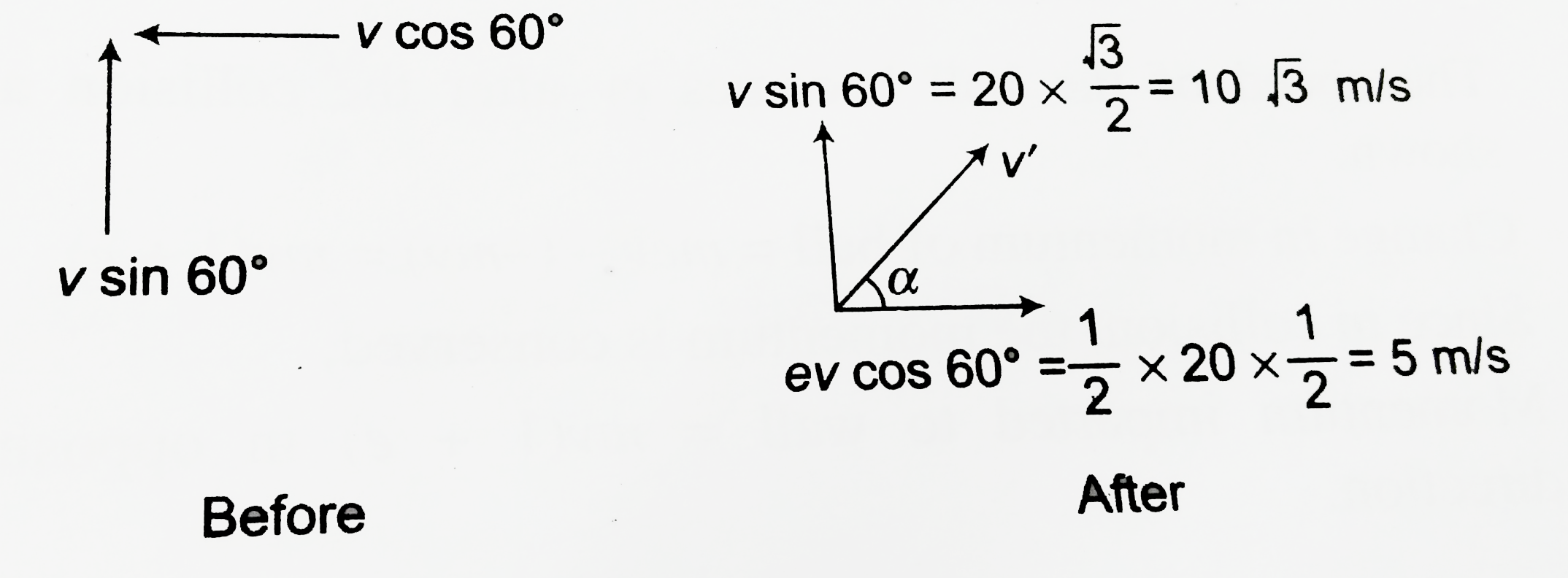
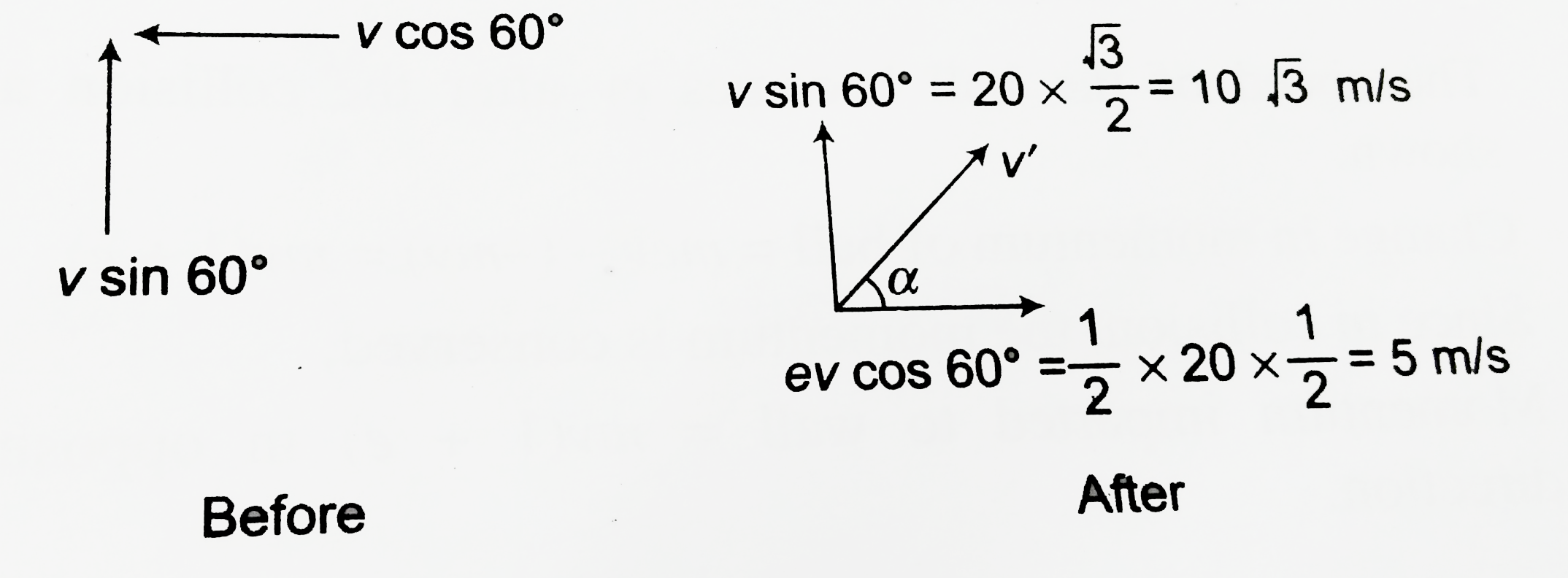
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the previous problem , if the collision is inelastic and the coefficient of restitution is $e = 1 / 2$ , the momentum imparted to the way by the wall is
A $0.25 k g m / s$
B $0.50 k g m / s$
C $0.75 k g m / s$
D $1 k g m / s$
Question 2 - Select One
In previous problem, end correction is
A $0.2 c m$
B $0.3 c m$
C $0.4 c m$
D $0.6 c m$
Question 3 - Select One
In previous problem, the angle of dip is
A ${tan}^{- 1} (0.75)$
B ${tan}^{- 1} (0.5)$
C ${tan}^{- 1} (0.8)$
DNone of these

CP SINGH-CENTER OF MASS-Exercises

Home
Ask Doubt
Profile