An isolated capacitor of unknown capacitance has been charged to potential V0. This capacitor is then connected to an uncharged capacitor of capacity C. If common potential is V(<V0, find unknow capacitance.
Let the capacitance of first capacitor be C0,
C1=C0,V1=V0,C2=C,V2=0,V=V
common potential:
V=C1V1+C2V2C1+C2
=C0V0+C×0C0+C
C0V+CV=C0V0⇒CV=C0(V0−V)
C0=CVV0−V
Topper's Solved these Questions
Similar Questions
A capacitor of capacity C charged to potential "V" and " then connected to an identical uncharged capacitor then loss of energy is
View SolutionA capacitor of capacity 20microF is charged upto 50V and and disconnected from cell. Now this charged capacitor is connected to another capacitor of capacitance C If final common potential is 20V then find the capacitance C.
View Solution
Knowledge Check
- Question 1 - Select One
A capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
A12C0V20B13C0V20C16C0V20D18C0V20 - Question 2 - Select One
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1 - Question 3 - Select One
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
A capacitor of capacitance C is charged to a potential differece V0. The terminals of the charged capacitor are then connected to those of an uncharged capacitor of capacitance C/2.
a. Compute the original charge of the system.
b. Find the final potential differce across each capacitor.
c. Find the final energy of the system.
d. Calculate the decrease in energy when the capacitors are connected.
e. Where did the ''lost'' energy go?View SolutionA parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
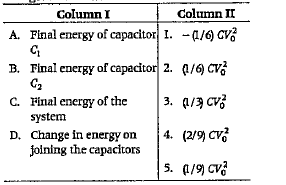
View SolutionA capacitor C1 of capacitance C is charged to a potential difference V0. The terminal of the charged capacitor are then connected to an uncharged capacitor C2of capacitance C/2. Match the entries of Column I with the entries of Column II and choose the correct option from the codes given below.
 View Solution
View SolutionA capacity of capacity C1 is charged up to V volt and then connected to an uncharged capacitor of capacity C2. Then final potential difference across each will be
View SolutionA capacitor of capacitance C0 is charged to a potential V0 and is connected with another capacitor of capacitance C as Shown . After closing the switch S, the common potential across the two capacitors becomes V . The capacitance C is given by
 View Solution
View Solution
