A parallel plate capacitor (C=50μF.d=4mm) is charged to 200V and then charging battery is removed. Now a dielectric slab (K=4) of thickness 2mm is placed between the plates. Find new potential difference across capacitor.
To solve the problem, we need to find the new potential difference across a parallel plate capacitor after inserting a dielectric slab. Here’s a step-by-step solution:
Step 1: Calculate the initial charge on the capacitor
The initial capacitance C is given as 50μF and the initial voltage V is 200V.
The charge Q stored in the capacitor can be calculated using the formula:
Q=C×V
Substituting the values:
Q=50×10−6F×200V=10×10−3C=10mC
Step 2: Determine the new capacitance with the dielectric slab
The dielectric slab has a dielectric constant K=4 and a thickness of 2mm. The total distance between the plates is d=4mm.
When the dielectric slab is inserted, it effectively divides the capacitor into two capacitors in series:
1. Capacitor C1 with the dielectric slab of thickness 2mm
2. Capacitor C2 with air gap of thickness 2mm
The capacitance of C1 is given by:
C1=Kϵ0Ad1=4ϵ0A2×10−3=2ϵ0A10−3
The capacitance of C2 is given by:
C2=ϵ0Ad2=ϵ0A2×10−3
Step 3: Express C1 and C2 in terms of C
The original capacitance C is:
C=ϵ0Ad=ϵ0A4×10−3
Thus, we can express C1 and C2 as:
C1=2C(since d1=2mm)
C2=C2(since d2=2mm)
Step 4: Calculate the equivalent capacitance C′
The total capacitance C′ of the series combination of C1 and C2 is given by:
1C′=1C1+1C2
Substituting the values:
1C′=12C+2C=1+42C=52C
Thus,
C′=2C5
Step 5: Calculate the new potential difference V′
Using the relationship Q=C⋅V and knowing that the charge Q remains constant:
Q=C⋅V=C′⋅V′
Substituting the values:
10mC=2C5⋅V′
Rearranging gives:
V′=10mC⋅52C
Substituting C=50μF=50×10−6F:
V′=10×10−3⋅52×50×10−6=50×10−3100×10−6=125V
Final Answer
The new potential difference across the capacitor is 125V.
The initial capacitance C is given as 50μF and the initial voltage V is 200V.
Q=C×V
Substituting the values:
Q=50×10−6F×200V=10×10−3C=10mC
The dielectric slab has a dielectric constant K=4 and a thickness of 2mm. The total distance between the plates is d=4mm.
1. Capacitor C1 with the dielectric slab of thickness 2mm
2. Capacitor C2 with air gap of thickness 2mm
C1=Kϵ0Ad1=4ϵ0A2×10−3=2ϵ0A10−3
C2=ϵ0Ad2=ϵ0A2×10−3
The original capacitance C is:
C=ϵ0Ad=ϵ0A4×10−3
C1=2C(since d1=2mm)
C2=C2(since d2=2mm)
The total capacitance C′ of the series combination of C1 and C2 is given by:
1C′=1C1+1C2
Substituting the values:
1C′=12C+2C=1+42C=52C
Thus,
C′=2C5
Using the relationship Q=C⋅V and knowing that the charge Q remains constant:
Q=C⋅V=C′⋅V′
Substituting the values:
10mC=2C5⋅V′
Rearranging gives:
V′=10mC⋅52C
Substituting C=50μF=50×10−6F:
V′=10×10−3⋅52×50×10−6=50×10−3100×10−6=125V
The new potential difference across the capacitor is 125V.
Topper's Solved these Questions
Similar Questions
The capacitance of a parallel plate capacitor is 50 pF and the distance between the plates is 4mm. It is charged to 200 V and then the charging battery is removed. Now a dielectric slab (κ=4) of thickness 2mm is placed. Determine (i) final charge on each plate (ii) finial potential difference between the plates (iii) final energy is the capacitor.
View SolutionA parallel plate capacitor is charged by a battery . After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates . How will potential difference between the plates ? Justify your answer
View Solution
Knowledge Check
- Question 1 - Select One
After charging a capacitor the battery is removed. Now by placing a dielectric slab between the plates
Athe potential difference between the plates and the energy stored will decreases but the charge on plates will remains sameBthe charge on the plates will decreases and the potential difference between the plates will increasesCthe potential difference between the plates will increases and energy stored will decreases but the charge on the plates will remains sameDthe potential difference, energy stored and the charge will remain unchanged - Question 2 - Select One
A capacitor with plate separation d is charged to V volts. The battery is disconnected and a dielectric slab of thickness d2 and dielectric constant '2' is inserted between the plates. The potential difference across its terminals becomes
AVB2 VC4V3D3V4 - Question 3 - Select One
Two identical parallel plate capacitors are connected in series to a battery of 100V. A dielectric slab of dielectric constant 4.0 is inserted between the plates of second capacitor. The potential difference across the capacitors will now be respectively
A50V,50VB80V,20VC20V,80VD75V,25V
A parallel plate capacitor is charged to a certain potential difference and the battery used to charged it is disconnected. Now a dielectric slab of dimensions equal to spacing between plates is introduced between the plates. What will be the changes, if any, in the charge, potential difference, capacitance, electric field strength and the energy stored in the capacitor?
View SolutionA parallel plate capacitor is charged by a battery . After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates . How will the capacitancee of the capacitor. ? Justify your answer
View SolutionThe space between plates of a parallel plate capacitor is filled by a dielectric and it is charged and then battery is removed. Now dielectric slab is slowly drawn out of the capacitor parallel to the plates. The variatiton of the potential of capacitor with respect to the length of the dielectric plate drawn out is
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
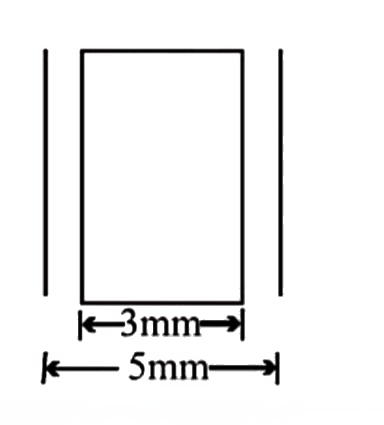 View Solution
View SolutionTwo identical parallel plate capacitors are connected in series and then joined in series will a batter of 100V. A slab of dielectric constant K=3 is inserted between the plates of the first capacitor. Then, the potential difference across the capacitor will be, respectively.
View Solution

