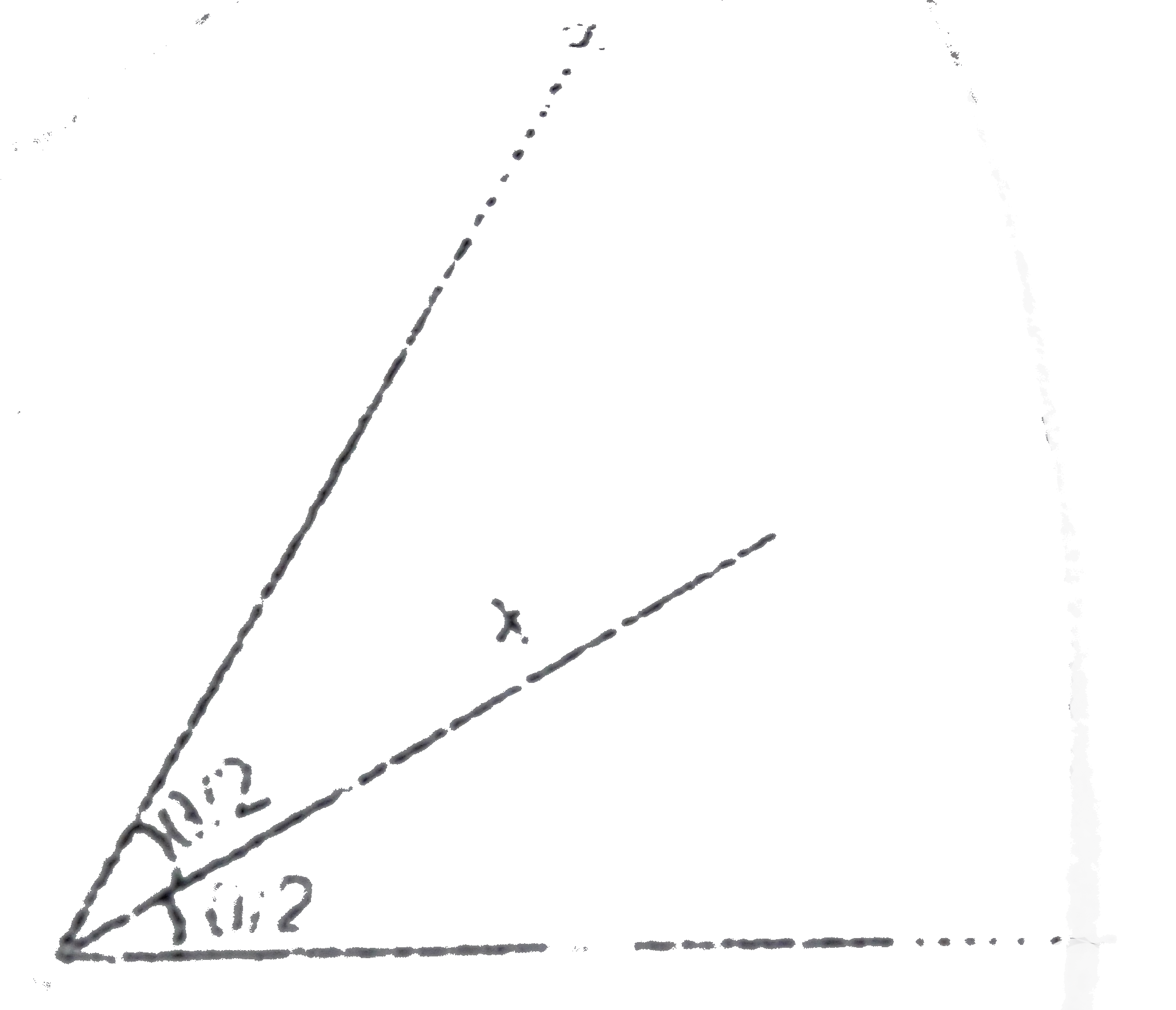
A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
μ0iπdcot(θ4),⊙
μ0i2πdcot(θ4),⊙
μ0i4πdcot(θ2),⊙
μ0i4πdcot(θ4),⊙
The correct Answer is:B
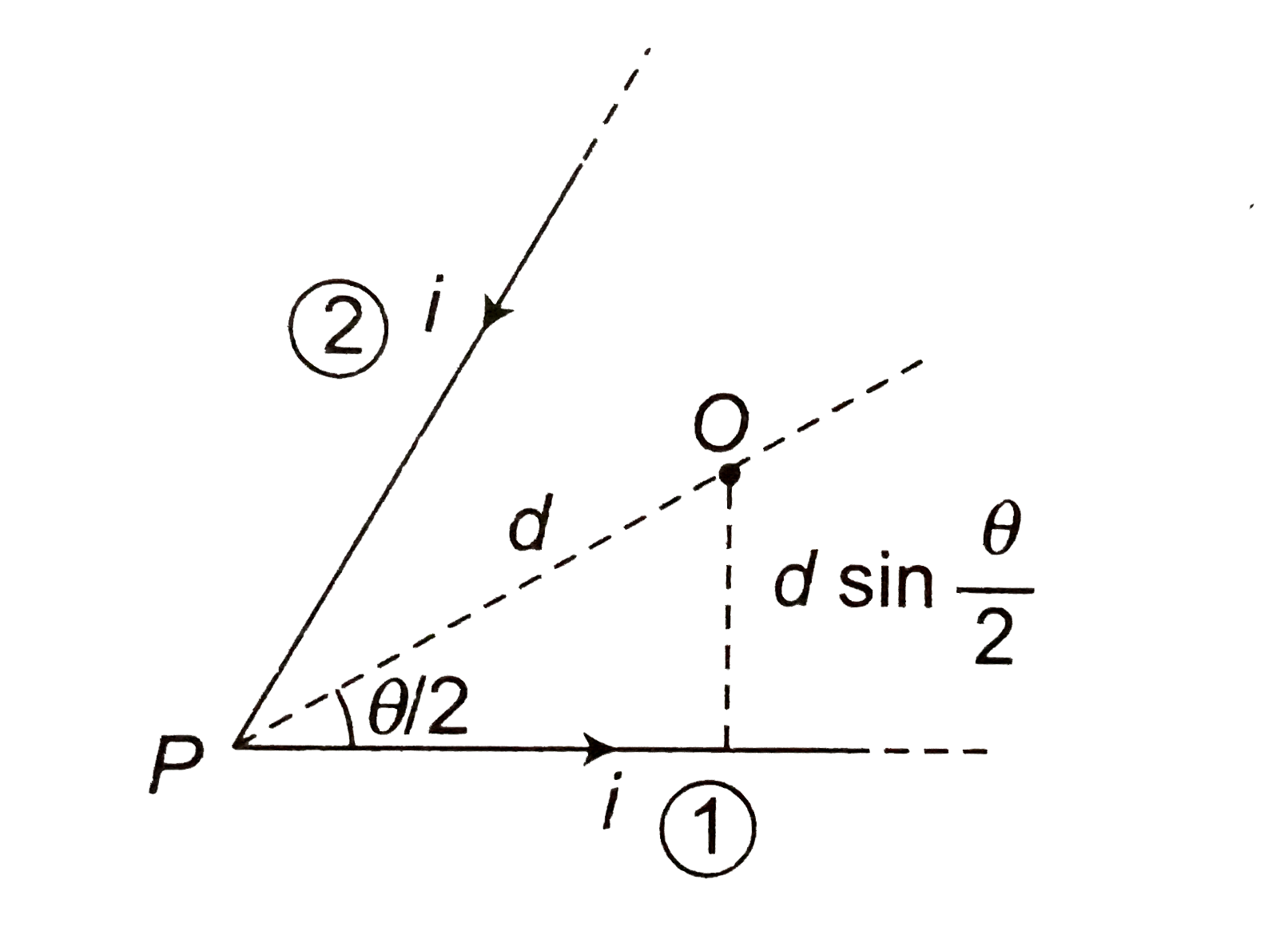
B1=μ0i4πdsin(θ2)[cos(θ2)+cos0]
=μ0i4πd{2sin(θ4)cos(θ4}){2cos2(θ4)−1+1}
=μ0i4πdcos(θ4)=B2,⊙
BO=B1+B2=μ0icot(θ4)2πd,⊙
Topper's Solved these Questions
Similar Questions
Alongwirecarry∈gacurrentiisbent→formapla≠∠α. F∈dthemag≠ticfieldBatap∮onthebisec→rofthis∠situatedatadistancexomthevertex.
View SolutionFind magnitude and direction of magnetic field at point P in the following cases.
(a)
(b)
P is the centre of square.
(c)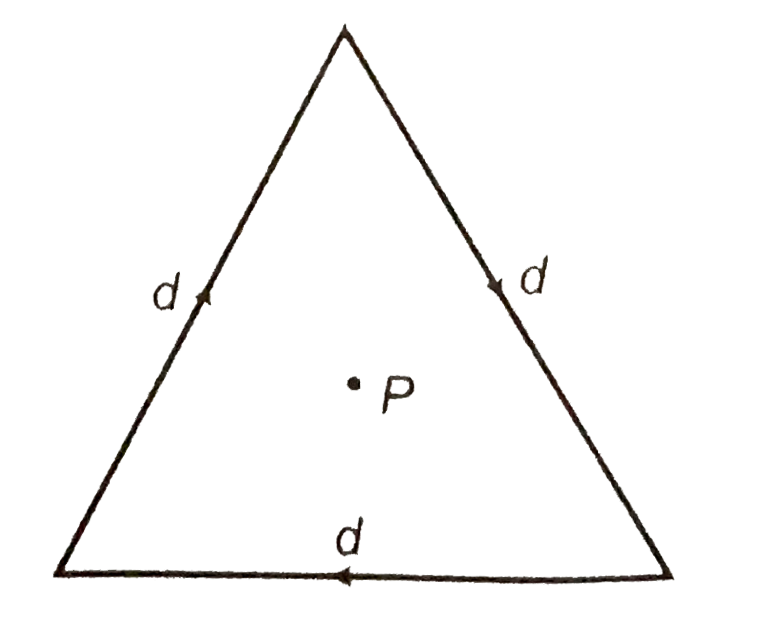
P is the centre of equilateral triangle.
(d)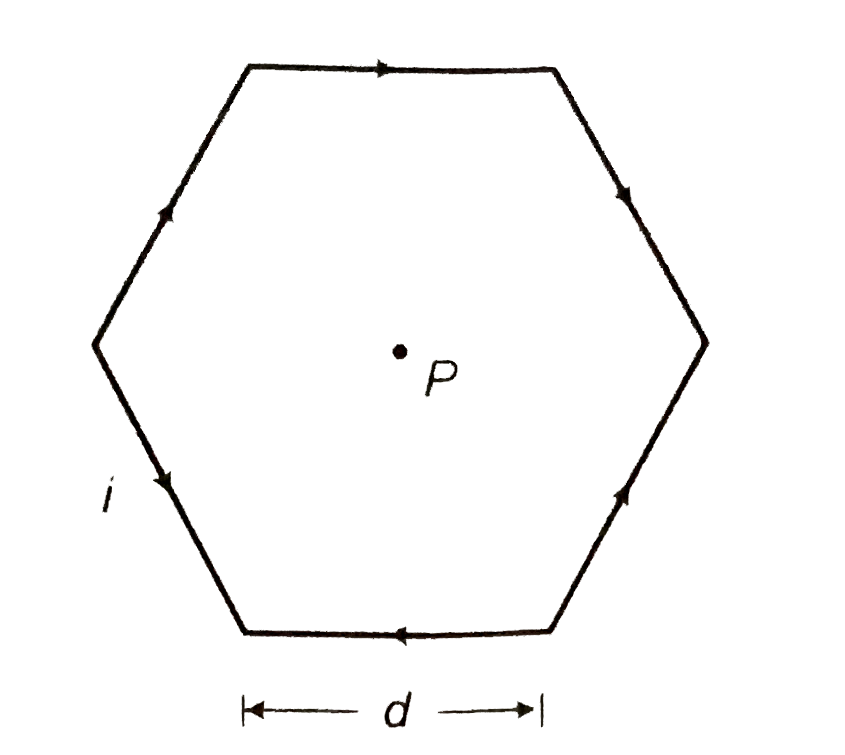
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)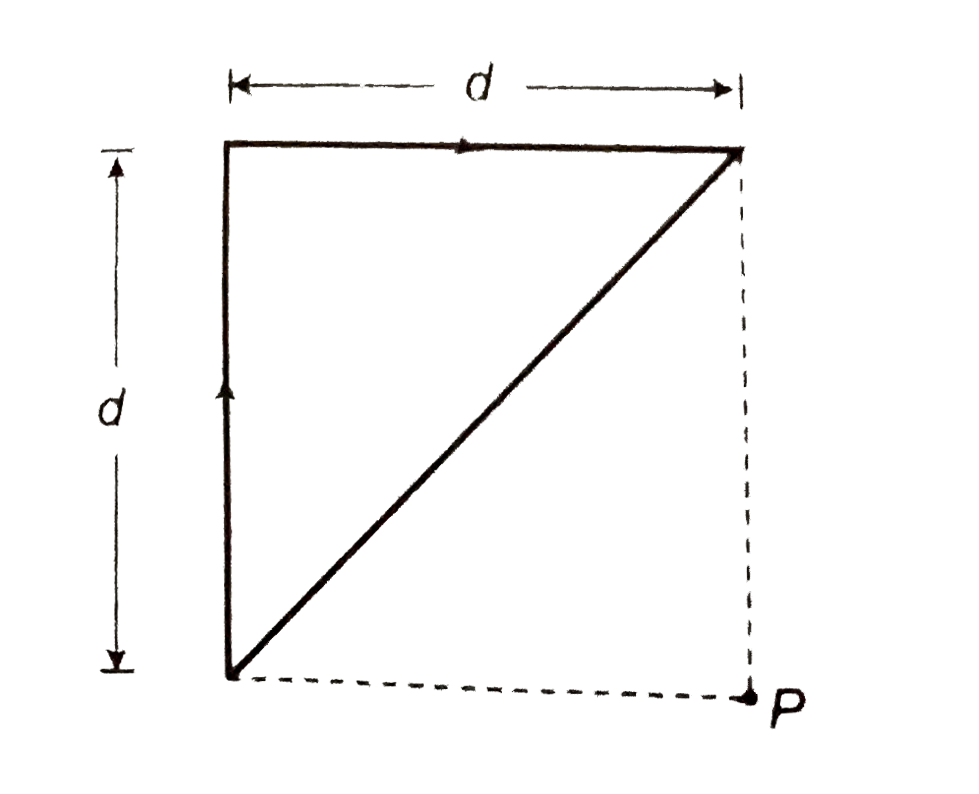
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
View Solution
Knowledge Check
A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
 Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙
Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙A long wire carrying a current i is bent to form a plane angle. The magnitude of magnetic field at height d, above the point of bending
A√2μ0i4πdB3√2μ0i4πdC5√2μ0i4πdD7√2μ0i4πdA long conducting wire carrying a current I is bent at 120∘( see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is
(μ0 is the permeability of free space)
 A2μ0I2πdBμ0I2πdCμ0I√3πdD√3μ0I2πd
A2μ0I2πdBμ0I2πdCμ0I√3πdD√3μ0I2πd
Find magnetic field at point P shown in Fig. point P is on the bisector of angle between the wires.
View SolutionFigure4.18 shows a current carrent carrying wire bent at an angle α. Find magentic induction at a point P located on the angle bisector at a distance x from the point O at the bend.

View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View Solution(i) A very long wire carrying a current I is bent at right angles .Find magnetic field at a point lying on a perpendicular to the wire , drawn through the point of bending at a distance d from it
(ii) Three long wires carrying same currect are placed as shown Find magnetic field at O.
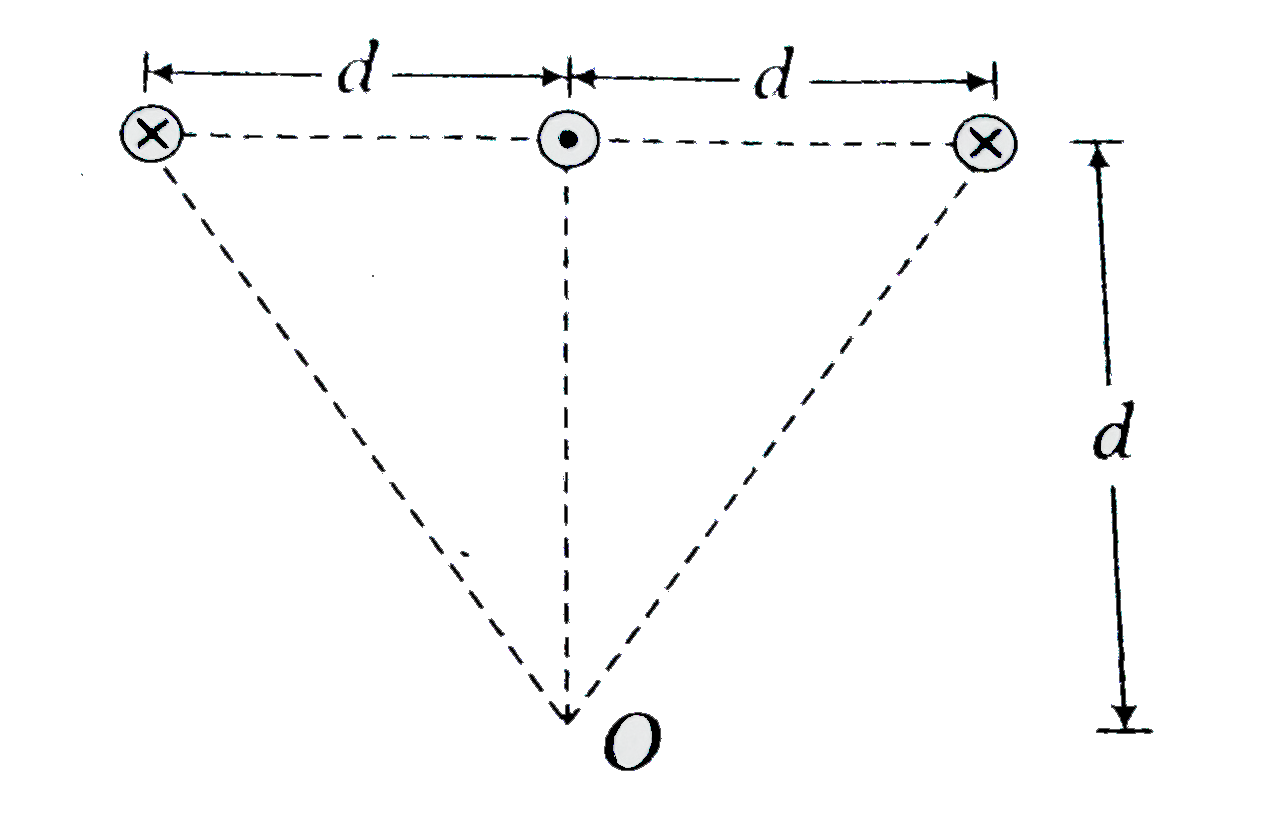
View SolutionA long straight wire, carrying current I, is bent at its midpoint to form an angle of 45∘. Find the induction of magnetic field at point P, distant R from the point of bending (as shown in)

View Solution
