a point charge q is situated at a distance r from one end of a thin conduction rod of length L having a charge Q (unifromly distributed a long its length).find the magnitudes of electric froce between the two.
To find the magnitude of the electric force between a point charge q and a thin conducting rod of length L with a uniformly distributed charge Q, we can follow these steps:
Step 1: Understand the Charge Distribution
The total charge Q is uniformly distributed along the length L of the rod. Therefore, the linear charge density λ can be defined as:
λ=QL
Step 2: Consider a Small Element of the Rod
Let’s consider a small segment of the rod of length dx at a distance x from the point charge q. The charge dq on this small segment can be expressed as:
dq=λdx=QLdx
Step 3: Calculate the Electric Force on the Small Segment
The electric force dF experienced by the small charge dq due to the point charge q is given by Coulomb’s law:
dF=kdq⋅qx2
Substituting dq from the previous step:
dF=k(QLdx)qx2=kQqLdxx2
where k is Coulomb's constant.
Step 4: Set Up the Integral for Total Force
To find the total force F on the rod, we need to integrate dF from x=r (the distance from the point charge to the start of the rod) to x=r+L (the distance from the point charge to the end of the rod):
F=∫r+LrdF=∫r+LrkQqLdxx2
Step 5: Perform the Integration
The integral can be computed as follows:
F=kQqL∫r+Lrdxx2
The integral ∫dxx2 evaluates to −1x:
F=kQqL(−1x)r+Lr=kQqL(−1r+L+1r)
Step 6: Simplify the Expression
This simplifies to:
F=kQqL(1r−1r+L)=kQqL((r+L)−rr(r+L))=kQqLLr(r+L)
Thus, the final expression for the electric force F is:
F=kQqr(r+L)
Final Answer
The magnitude of the electric force between the point charge q and the conducting rod with charge Q is:
F=14πϵ0Qqr(r+L)
The total charge Q is uniformly distributed along the length L of the rod. Therefore, the linear charge density λ can be defined as:
λ=QL
Let’s consider a small segment of the rod of length dx at a distance x from the point charge q. The charge dq on this small segment can be expressed as:
dq=λdx=QLdx
The electric force dF experienced by the small charge dq due to the point charge q is given by Coulomb’s law:
dF=kdq⋅qx2
Substituting dq from the previous step:
dF=k(QLdx)qx2=kQqLdxx2
where k is Coulomb's constant.
To find the total force F on the rod, we need to integrate dF from x=r (the distance from the point charge to the start of the rod) to x=r+L (the distance from the point charge to the end of the rod):
F=∫r+LrdF=∫r+LrkQqLdxx2
The integral can be computed as follows:
F=kQqL∫r+Lrdxx2
The integral ∫dxx2 evaluates to −1x:
F=kQqL(−1x)r+Lr=kQqL(−1r+L+1r)
This simplifies to:
F=kQqL(1r−1r+L)=kQqL((r+L)−rr(r+L))=kQqLLr(r+L)
Thus, the final expression for the electric force F is:
F=kQqr(r+L)
The magnitude of the electric force between the point charge q and the conducting rod with charge Q is:
F=14πϵ0Qqr(r+L)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - C.U.Q133videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1(C.W)24videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS14videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type6videos
EXPERIMENTAL PHYSICS
Similar Questions
A thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.
 View Solution
View SolutionA wire of length L carries charge Q uniformly distributed along its length. Find the electric field at a distance √3L2 from the wire at point A as shown.
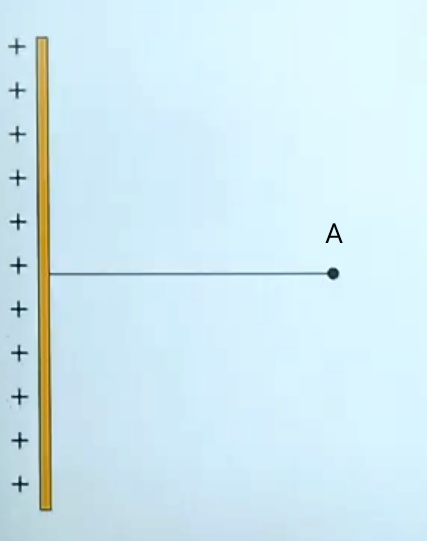 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rod of length l having uniformly distributed charge Q is rotated about one end with constant frequency f Its magnetic moment
AπfQl2BπfQl23C2πfQl23D2πRQ2 - Question 2 - Select One
A 10 cm long rod carries a charge of +150μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both the ends of the rod.
A15.6×107N/CB15.6×105N/CC1.56×107N/CD1.56×105N/C - Question 3 - Select One
A charge +q is situated at a distance 'd' away from both the sides of a grounded conducting 'L' shaped sheet as shown in the figure.
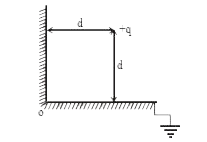
The force acting on the charge +q isAtowards O, magnitude q232πε0d2(2√2+1)Baway from O, magnitude q232πε0d2(2√2+1)Ctowards O, magnitude q232πε0d2(2√2−1)Daway from O, magnitude q232πε0d2(2√2−1)
A point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionA point charge q is placed at a distance d from centre of a uniformly charged conducting spherical shell of radius R and having charge Q as shown. Magnitude of electric field intensity at point P just inside the shell due to charge on shell is
View SolutionDraw a plot showing variation of electric field with distance from the centre of a solid conducting sphere of radius R having a charge Q on its surface.
View SolutionA particle of mass m is situated at a distance d from one end of a rod of mass M and length L as shown in diagram. Find the magnitude of the gravitational force between them
 View Solution
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity ω about its end, compute its magnetic moment.
 View Solution
View Solution

