Two charge $+ Q$ each are placed at the two verticles of an equilateral triangle of side $a$ .The intensity of electric field at the third vertex is

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the intensity of the electric field at the third vertex of an equilateral triangle with two charges $+ Q$ at the other two vertices, we can follow these steps:
1. Understanding the Configuration:
- We have an equilateral triangle with vertices A, B, and C.
- Charges $+ Q$ are placed at vertices A and B.
- We need to find the electric field at vertex C due to these two charges.
2. Calculating Electric Field Due to One Charge:
- The electric field $E$ due to a point charge $Q$ at a distance $r$ is given by the formula:
$E = \frac{k Q}{r^{2}}$
- Here, the distance $r$ from either charge to vertex C is equal to the side length $a$ of the triangle.
3. Electric Field at Vertex C from Each Charge:
- The electric field at vertex C due to charge at A (denote as $E_{A}$ ) is:
$E_{A} = \frac{k Q}{a^{2}}$
- The electric field at vertex C due to charge at B (denote as $E_{B}$ ) is:
$E_{B} = \frac{k Q}{a^{2}}$
4. Direction of Electric Fields:
- The electric field $E_{A}$ points away from charge A towards C.
- The electric field $E_{B}$ points away from charge B towards C.
- The angle between $E_{A}$ and $E_{B}$ is $60^{\circ}$ because of the geometry of the equilateral triangle.
5. Calculating the Resultant Electric Field:
- To find the net electric field $E_{n e t}$ at vertex C, we use the vector addition of $E_{A}$ and $E_{B}$ :
$E_{n e t} = \sqrt{E_{A}^{2} + E_{B}^{2} + 2 E_{A} E_{B} cos (60^{\circ})}$
- Since $E_{A} = E_{B} = \frac{k Q}{a^{2}}$ and $cos (60^{\circ}) = \frac{1}{2}$ :
$E_{n e t} = \sqrt{{(\frac{k Q}{a^{2}})}^{2} + {(\frac{k Q}{a^{2}})}^{2} + 2 (\frac{k Q}{a^{2}}) (\frac{k Q}{a^{2}}) (\frac{1}{2})}$
- Simplifying this:
$E_{n e t} = \sqrt{2 {(\frac{k Q}{a^{2}})}^{2} + {(\frac{k Q}{a^{2}})}^{2}}$
$= \sqrt{3 {(\frac{k Q}{a^{2}})}^{2}}$
$= \frac{k Q \sqrt{3}}{a^{2}}$
6. Final Expression:
- Substituting $k = \frac{1}{4 π ϵ_{0}}$ :
$E_{n e t} = \frac{\sqrt{3} Q}{4 π ϵ_{0} a^{2}}$
Final Answer:
The intensity of the electric field at the third vertex is:
$E_{n e t} = \frac{\sqrt{3} Q}{4 π ϵ_{0} a^{2}}$

Updated on:7/8/2024

Equal charges $q$ are placed at the vertices $A$ and $B$ of an equilatral triangle $A B C$ of side $a$ . The magnitude of electric field at the point $C$ is
A $\frac{q}{4 π ε_{0} a^{2}}$
B $\frac{\sqrt{2} q}{4 π ε_{0} a^{2}}$
C $\frac{\sqrt{3} q}{4 π ε_{0} a^{2}}$
D $\frac{q}{2 π ε_{0} a^{2}}$
A total charge q is divided as $q_{1}$ and $q_{2}$ which are kept at two of the vertices of an equilateral triangle of side a. The magnitude of the electric field E at the third vertex of the triangle is to be depicted schematically as a function of $x = q_{1} / q$ . Choose the correct figure.
A
B
C
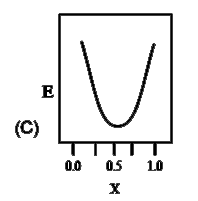D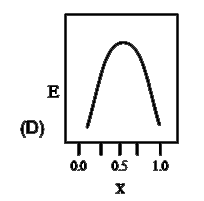
Three point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
A $(\frac{\sqrt{3}}{4 π ε_{0}}) {(\frac{q}{a})}^{2}$
B $(\frac{\sqrt{2}}{4 π ε_{0}}) {(\frac{q}{a})}^{2}$
C $(\frac{\sqrt{3}}{4 π ε_{0}}) {(\frac{q}{2 a})}^{2}$
D $(\frac{\sqrt{2}}{4 π ε_{0}}) {(\frac{2 q}{a})}^{2}$