Three charges each20μC are placed at the corners of an equilateral triangle of side 0.4m The potential energy of the system is
18×10−6J
9J
9×10−6J
27J
The correct Answer is:4
To find the potential energy of a system of three charges placed at the corners of an equilateral triangle, we can follow these steps:
1. Identify the Charges and Distance:
- Given three charges q1=q2=q3=20μC=20×10−6C.
- The side length of the equilateral triangle L=0.4m.
2. Formula for Potential Energy:
- The potential energy U of a system of point charges is given by the formula:
U=k(q1q2r12+q2q3r23+q3q1r31)
- Here, k is Coulomb's constant, k=9×109Nm2/C2, and rij is the distance between charges qi and qj.
3. Calculate Each Pair's Contribution:
- Since all charges are equal and the distances are the same:
U=k(q2L+q2L+q2L)=3⋅kq2L
- Substitute q=20×10−6C and L=0.4m:
U=3⋅9×109⋅(20×10−6)20.4
4. Calculate q2:
- Calculate (20×10−6)2=400×10−12C2.
5. Substitute Values:
- Now substitute back into the equation:
U=3⋅9×109⋅400×10−120.4
6. Simplify the Expression:
- Calculate the numerator:
9×109⋅400×10−12=3600×10−3=3.6J
- Now divide by 0.4:
U=3⋅3.60.4=3⋅9=27J
7. Final Result:
- The potential energy of the system is:
U=27J
- Given three charges q1=q2=q3=20μC=20×10−6C.
- The side length of the equilateral triangle L=0.4m.
- The potential energy U of a system of point charges is given by the formula:
U=k(q1q2r12+q2q3r23+q3q1r31)
- Here, k is Coulomb's constant, k=9×109Nm2/C2, and rij is the distance between charges qi and qj.
- Since all charges are equal and the distances are the same:
U=k(q2L+q2L+q2L)=3⋅kq2L
- Substitute q=20×10−6C and L=0.4m:
U=3⋅9×109⋅(20×10−6)20.4
- Calculate (20×10−6)2=400×10−12C2.
- Now substitute back into the equation:
U=3⋅9×109⋅400×10−120.4
- Calculate the numerator:
9×109⋅400×10−12=3600×10−3=3.6J
- Now divide by 0.4:
U=3⋅3.60.4=3⋅9=27J
- The potential energy of the system is:
U=27J
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level III (C.W)55videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 18videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1(C.W)24videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS14videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type6videos
EXPERIMENTAL PHYSICS
Similar Questions
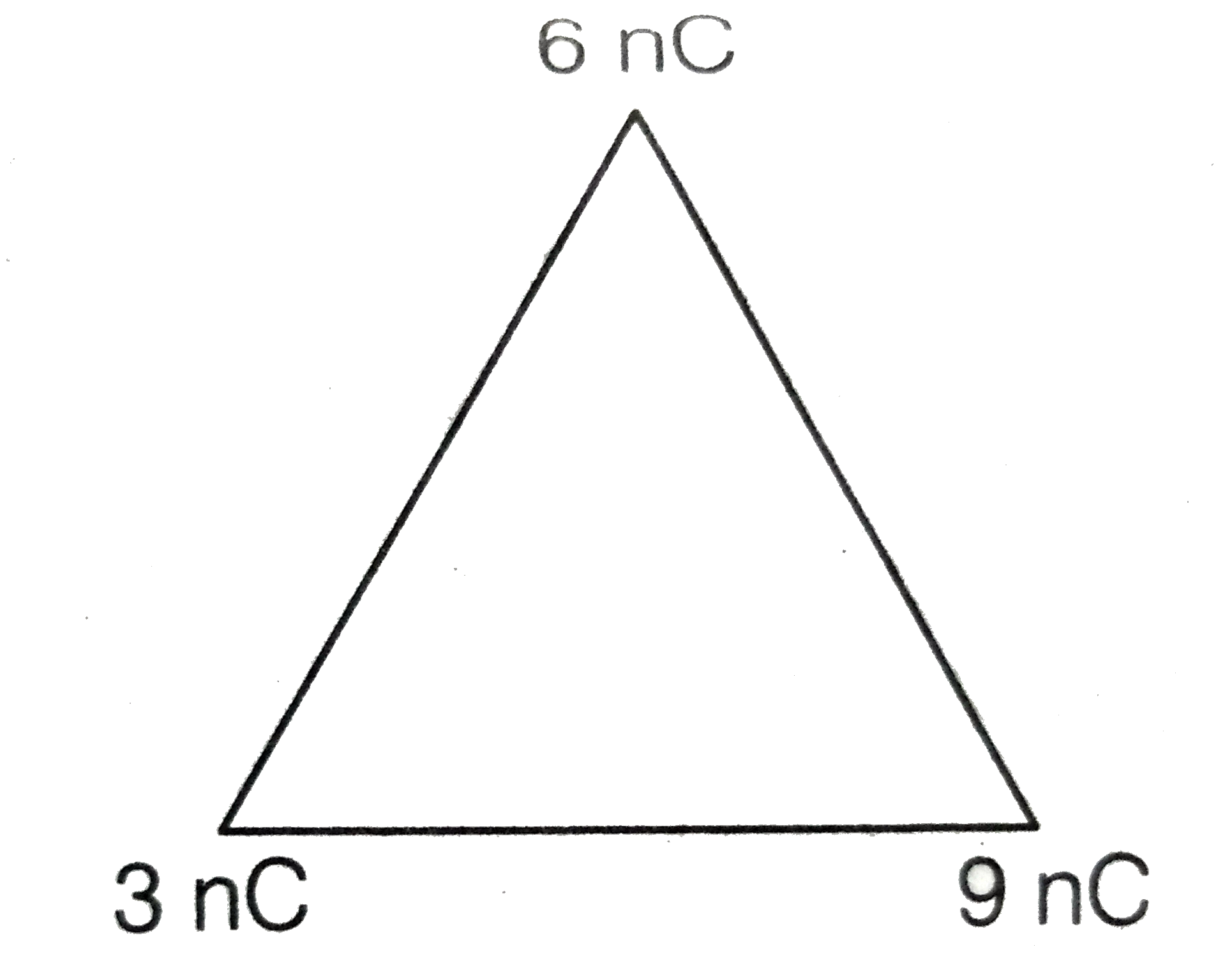
Three point charges 3nC, 6nC and 6nC are placed at the corners of an equilateral triangle of side 0.1 m. The potential energy of the system is
 View Solution
View SolutionThree charges +q,+qand−q are located at the corners of an equilaterial triangle of side a. Calculate potential energy of the system.
View Solution
Knowledge Check
- Question 1 - Select One
Three particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
A3GMa2B3GM2aC−3GM2a2D3GM2a - Question 2 - Select One
Three particles, each having a charge of 10μC are placed at the coners of an equilateral triangle of side 10cm. The electrostatic potential energy of the system is (Given 14πε0=9×109N−m2/C2)
AZeroBInfiniteC27JD100J - Question 3 - Select One
Three particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
A−3Gm22bB−Gm22bC−3Gm2bD−Gm2b
Three equal charges q are placed at the corners of an equilateral triangle of side a.
(i) Find out potential energy of charge system.
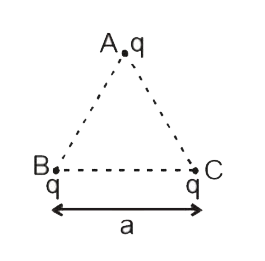
(ii) Calculate work required to decrease the side of triangle to a/2.
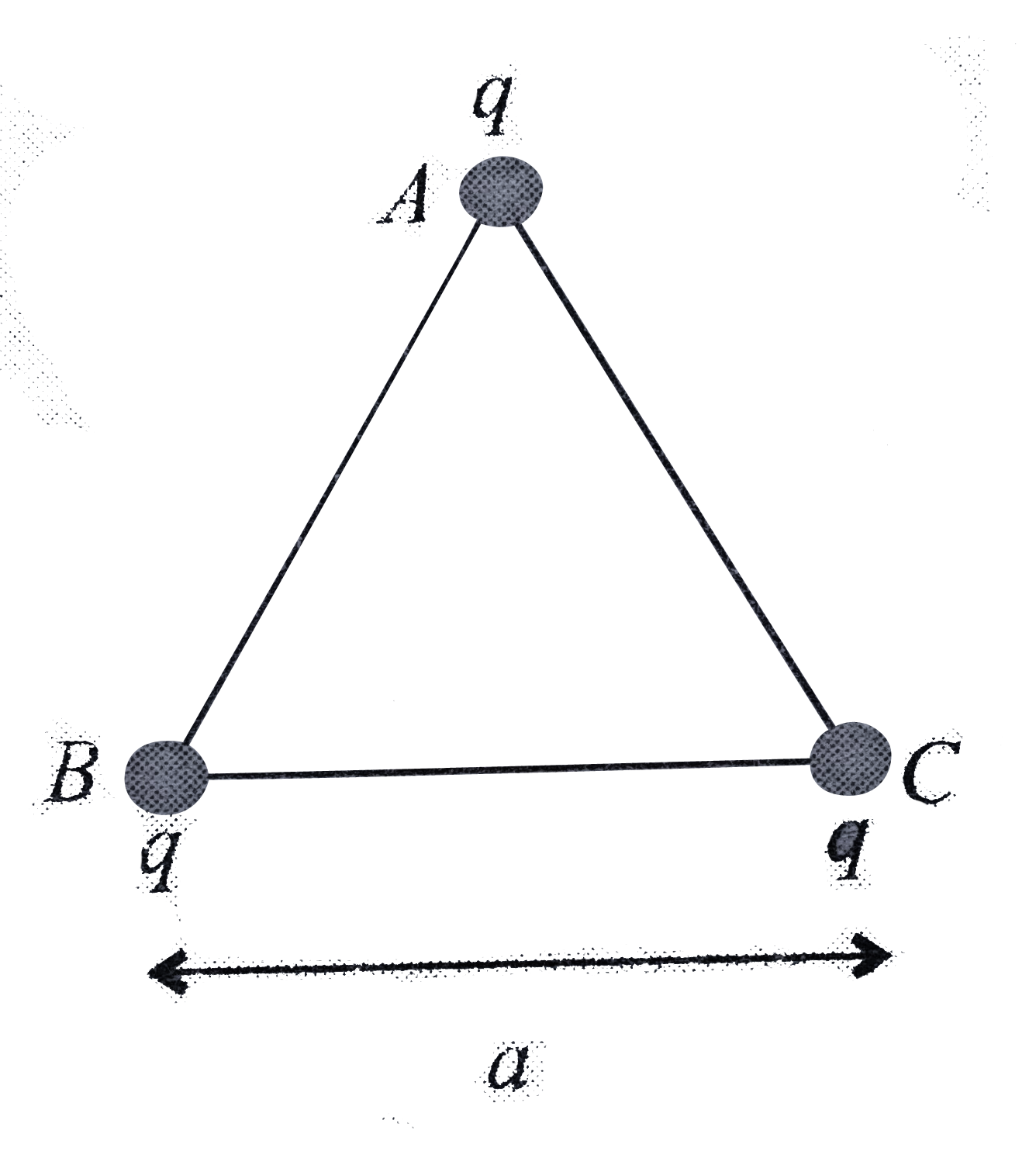
(iii) If the charges are released from the shown position and each of them has same mass m then find the speed of each particle when they lie on triangle of side 2a.View SolutionThree equal charges q are placed at the corners of an equilateral triangle of side A.
(i) Find out potential energy of charge system.
(ii) Calculate work required to decrease the side of triangle to a/2.
(iii) If the charges are released from the shown position and each of them has same mass m, then find the speed of each particle when they lie on triangle of side 2a.
 .View Solution
.View SolutionCharges of +4μC,−6μCand−16μC are placed in air at the corners of an equilateral triangle of side 10. find the potential energy of the system. −0.72J
View SolutionThree point charges 2μC,3μCand5μC are placed at the corners of an equilateral triangle of side 200 cm. Calculate the potentail energy of the system.
View SolutionTwo identical charges are placed at the two corners of an equilateral triangle. The potential energy of the system is U. The work done in bringing an identical charge from infinity to the third vertex is
View Solution

