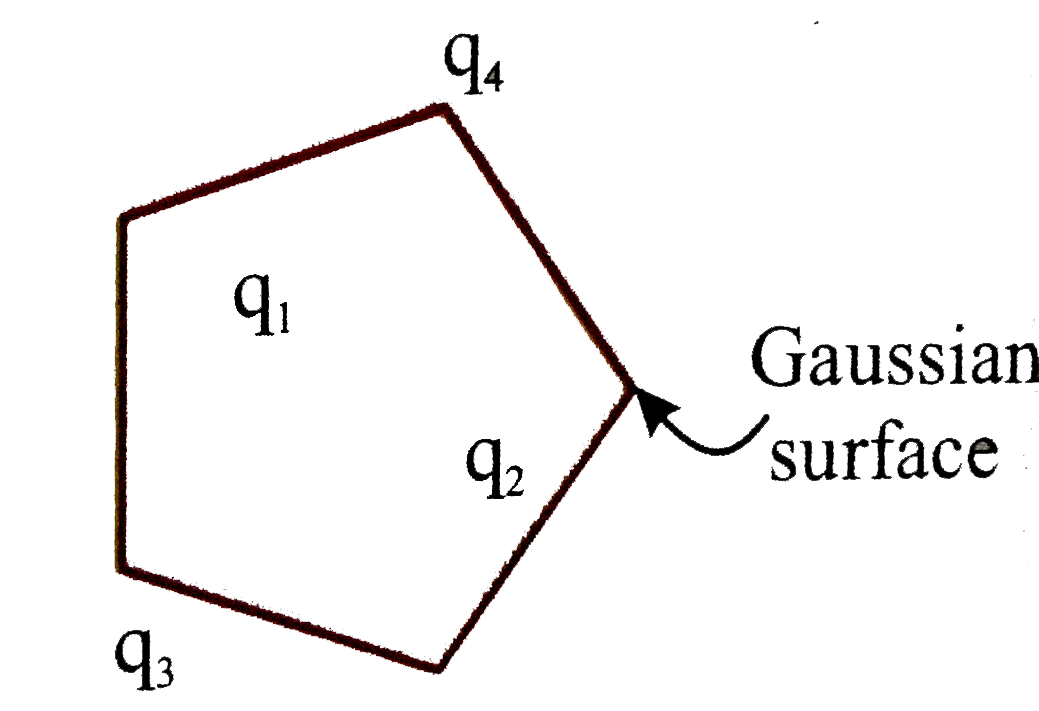
Assertion: Four point charges q1,q2,q3 and q4 are as shown in Fig,The flux over the shown Gaussians surface depends only on charges q1 and q2
Reason:Electric field at all points on Gaussians surface depends on any charges q1 and q2
Both (A) and (R) are true and 'R' is the correct explanation of A.
Both A and R are true and R is not the correct explanation of A
(A) is true but (R) is false
(A) is false but (R) is true
The correct Answer is:3
Step by step video, text & image solution for Assertion: Four point charges q_(1),q_(2),q_(3) and q_(4) are as shown in Fig,The flux over the shown Gaussians surface depends only on charges q_(1) and q_(2) Reason:Electric field at all points on Gaussians surface depends on any charges q_(1) and q_(2) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1(C.W)24videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level II(C.W)27videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question11videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS14videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type6videos
EXPERIMENTAL PHYSICS
Similar Questions
Assertion (A): Three point charges Q1,Q2 and Q3 are shown in the figure. The flux over the Gaussian surface depends on only one charge point.
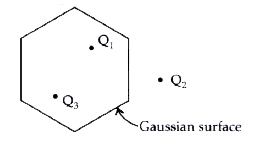
Reason (R): Electric flux depends on the all charges nearby.View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.View Solution
Knowledge Check
- Question 1 - Select One
The value of charge q1,q2andq3 as shown in the figure are
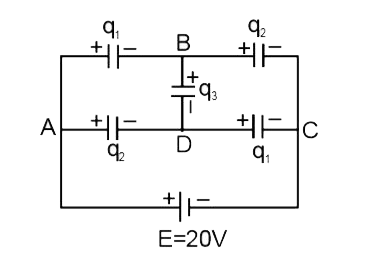 Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μC
Aq1=32μC,q2=24μC,q3=−8μCBq1=48μc,q2=16μC,q3=+8μCCq1=32μC,q2=24μC,q3=+8μCDq1=3μC,q2=4μC,q3=+2μC - Question 2 - Select One or More
Consider a Gaussian spherical surface covering a dipole of charge q and -q, then
 Aq∈=0 (net charge enclosed by the spherical surface)Bϕ≠t=0 (net flux coming out the spherical surface)CE=0 at all points on the spherical surface.D∫→E⋅d→s = 0 (surface integral of over the spherical surface)
Aq∈=0 (net charge enclosed by the spherical surface)Bϕ≠t=0 (net flux coming out the spherical surface)CE=0 at all points on the spherical surface.D∫→E⋅d→s = 0 (surface integral of over the spherical surface) - Question 3 - Select One
Three charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
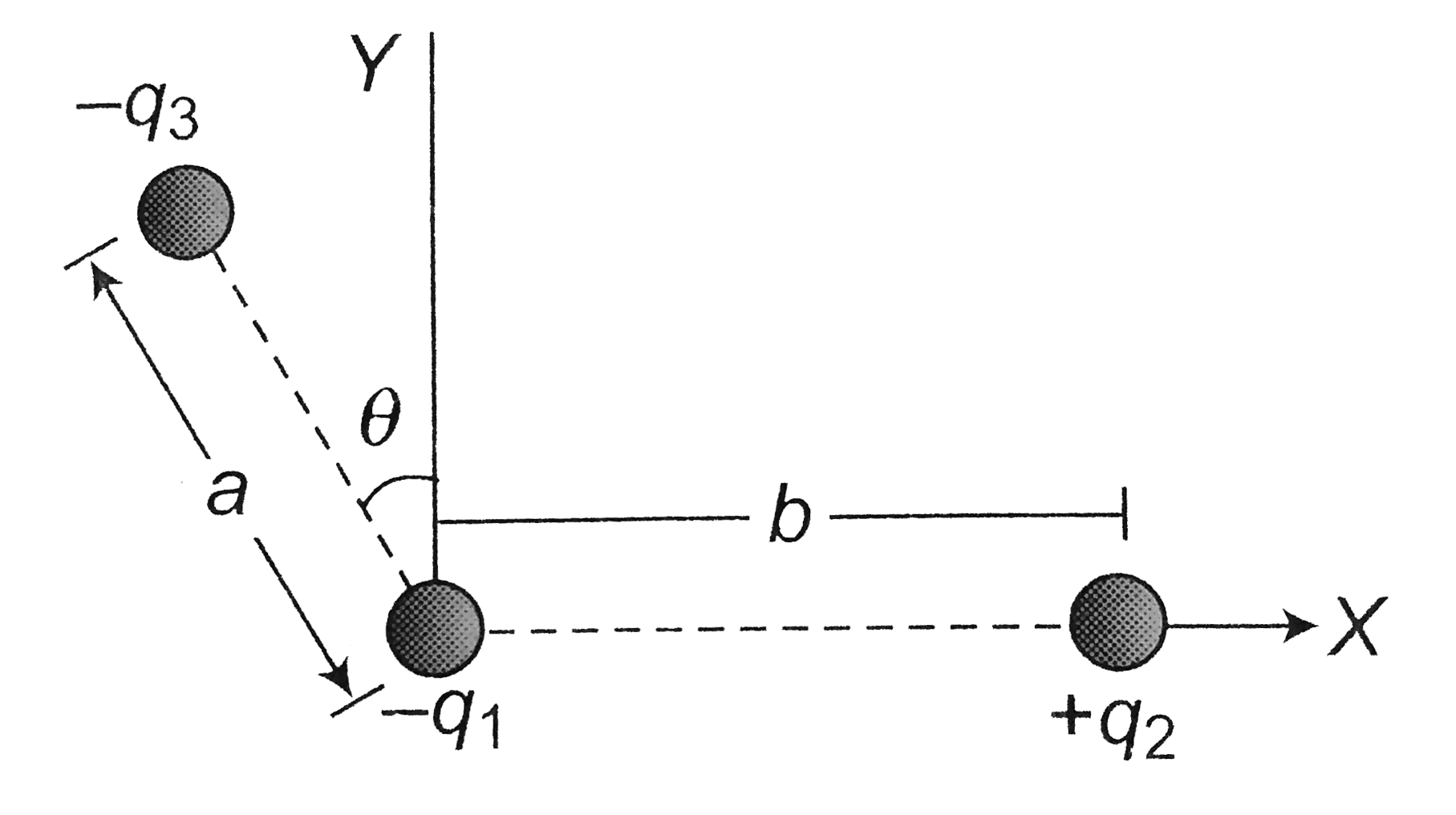 Aq2b2−q3a2sinθBq2b2−q3a2cosθCq2b2+q3a2sinθDq2b2+q3a2sinθ
Aq2b2−q3a2sinθBq2b2−q3a2cosθCq2b2+q3a2sinθDq2b2+q3a2sinθ
Three charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
 View Solution
View SolutionFigure shows four charges q1,q2,q3,andq4 fixed is space. Then the total flux of the electric field through a closed surface S, due to all the charges, is
 View Solution
View Solutionq1,q2,q3 and q4 are point charges located at point as shown in the figure and S is a spherical Gaussian surface of radius R. Which of the following is true according to the Gauss's law
 View Solution
View SolutionTwo charges q1 and q2 are kept on x-axis and electric field at different points an x-axis is plotted against x. Choose correct statement about nature and magnitudes of q1 and q2
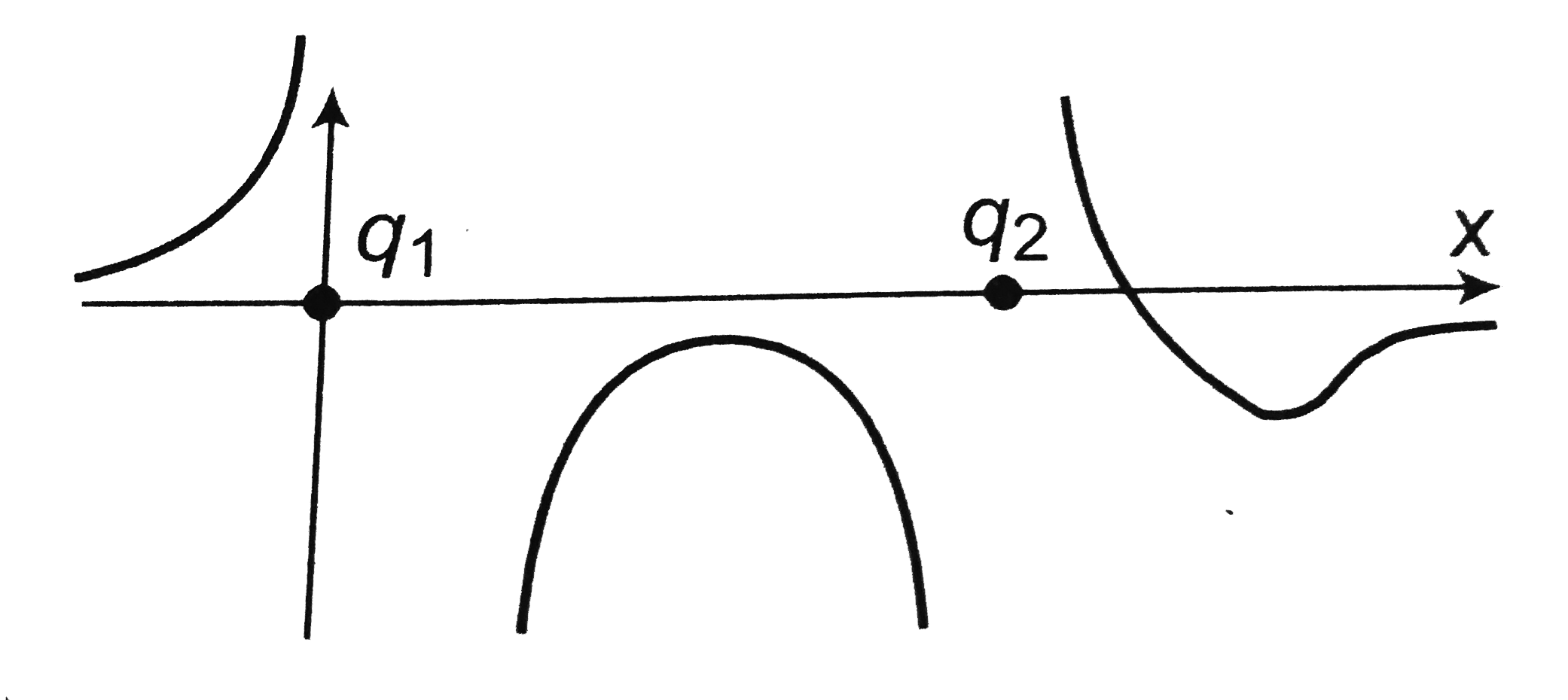 View Solution
View SolutionA Gaussian surface S encloses two charges q1=qandq2=−qthe field at p is
where →E1,→E2and→E3 are the field contributed by q1,q2andq3at P respectively.
 View Solution
View Solution

