A conducting sphere A of radius a ,with charge Q , is placed concentrically inside a conducting shell B of radius b . B is earthed. C is the common centre of the A and B
The field at a distance r form C where a≤r≤b is 14πε0Qr2
The potential at a distance r form C where a<r<b is 14πε0Qr
The potential difference between A and B is 14πε0(Q)(1a−1b)
The potentia at a distance r from C where a≤r≤b is ,14πε0Q(1r−1b)
The correct Answer is:A,C,D
E=14πε0qr0&V=14πε0qr
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Passage I3videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Passage II3videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - NCERT based Question14videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS14videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type6videos
EXPERIMENTAL PHYSICS
Similar Questions
A conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View SolutionA spherical conductor A of radius r is placed concentrically inside a conducting shell B of radius R(R>r). A charge Q is given to A , and then A is joined to B by a metal wire. The charge flowing from A to B will be
View Solution
Knowledge Check
- Question 1 - Select One
A conducting sphere A of radius a, with charge Q, is placed concentrically inside a conducting shell B of radius b. B is earthed. C is the common center of AandB. Study the following statements.
(i) The potential at a distance r from C, where
a≤r≤b,is14πε0(qr)
(ii) The potential difference between AandB is
14πε0Q(1r−1B)
(iii) The potential at a distance r from C, where
a≤r≤b,is14πε0Q(1r−1B)
Which of the above statements are correct ?
 .AOnly (i) and (ii)BOnly (ii) and (iii)COnly (i) and (iii)DAll of these
.AOnly (i) and (ii)BOnly (ii) and (iii)COnly (i) and (iii)DAll of these - Question 2 - Select One
A conducting sphere A of radius a, with charge Q is placed concentrically inside a conducting shell B of radius b. B is earthed, C is the common centre of A and B. If P is the point between shells A and B at distance r from center C then Match the proper entries from column-2 to column-1 using the codes given below the columns,
(use a=1m,b=3m,r=2m and K=14πεo)APQRS3124BPQRS1234CPQRS2341DPQRS3412 - Question 3 - Select One
A small conducting sphere of radius a, carrying a charge +Q, is placed inside an equal and oppositely charged conducting shell of radius b such that their centers coincide. Determine the potential at a point which is at a distance c from center such that a<c<b.
Ak(Q/c+Q/b)Bk(Q/a+Q/b)Ck(Q/a−Q/b)Dk(Q/c−Q/b)
A solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded

The charge on solid sphere isView SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded

The potential of outer shell isView SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded

Pick up the correct statement.View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin unchanged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
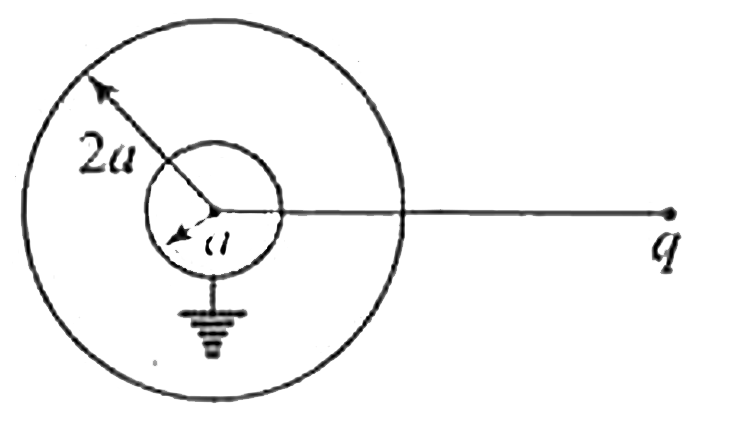
The charge on solid sphere is :View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin unchanged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
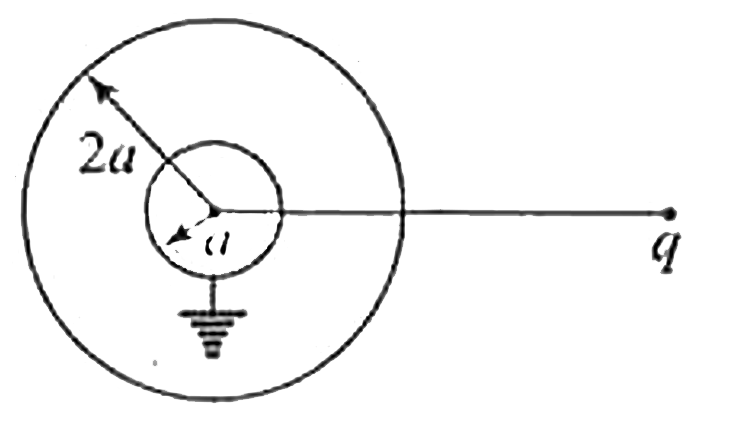
The potential of outer shell isView Solution

