Two wires AO and OC carry equal currents i as shown in Fig. One end of both the wires extends to infinity. Angle AOC is α. The magnitude of magnetic field is point P on the bisector of these two wires at a distance r from point O is

μ0i2πrcot(α2)
μ0i4πrcot(α2)
μ0i2πr(1+cos(α)2)sin(α2))
μ0i4πrsin(α2)
The correct Answer is:C
B=μ04πIa[sin(90−θ/2)+sin90∘]×2
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT Based Questions20videos
MOVING CHARGES AND MAGNETISM
- BOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-V (SINGLE ANSWER QUESTION)85videos
MOVING CHARGES AND MAGNETISM
- BOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level-II(C.W)63videos
MOVING CHARGES AND MAGNETISM
- BOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)17videos
MAGNETISM AND MATTER
- BOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)9videos
NUCLEAR PHYSICS
Similar Questions
Two wires CO and OA carry equal currents I as shown in figure. One end of both the wires extends to infinity. Given ∠AOC=θ. What is the magnitude of magnetic field induction at a point P at a distance r from O lying on the bisector of angle θ.
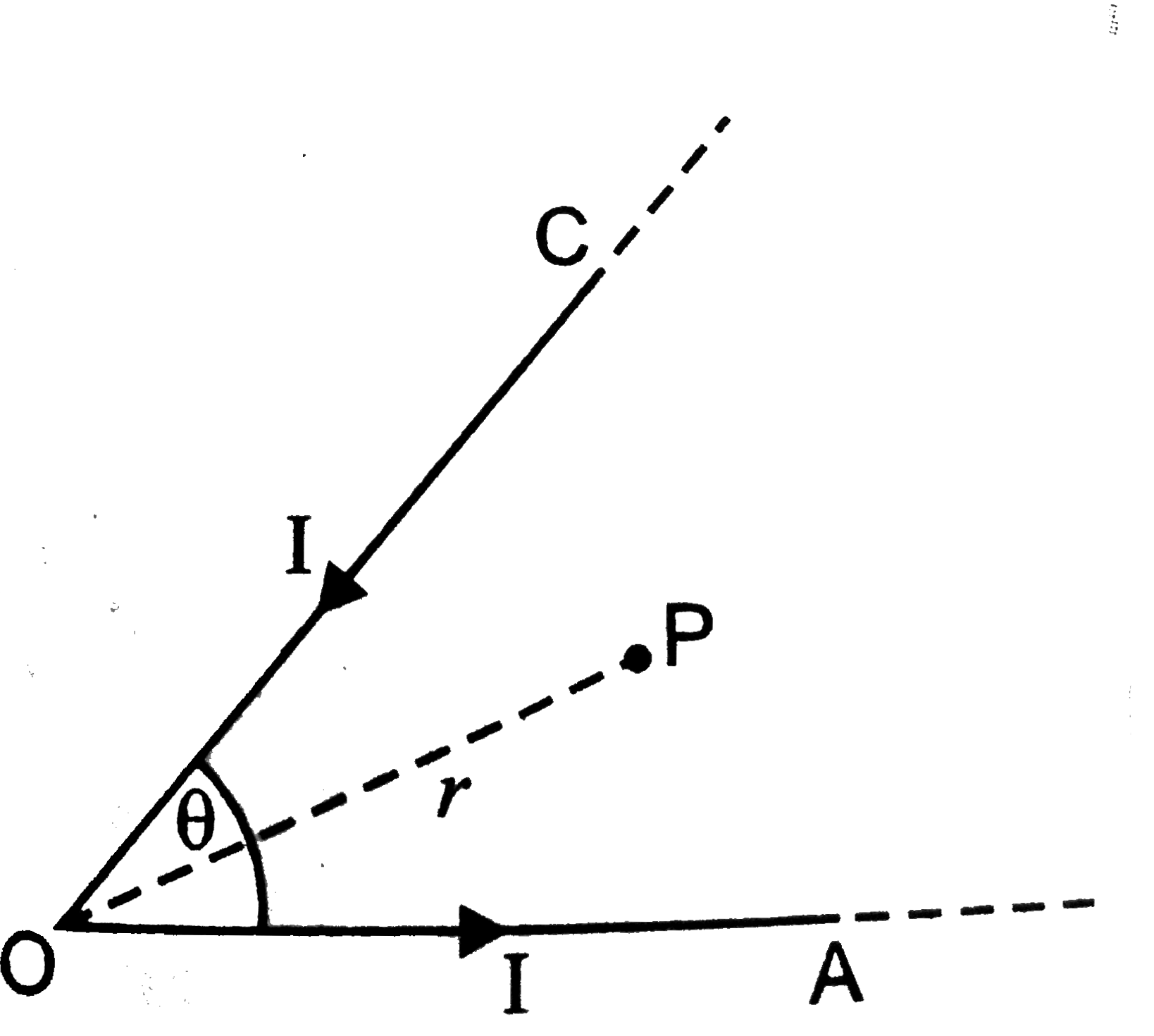 View Solution
View SolutionFind magnetic field at point P shown in Fig. point P is on the bisector of angle between the wires.
View Solution
Knowledge Check
- Question 1 - Select One
A current carrying wire is bent in the L shapes as shown in figure. The length of both arms extend to infinity. Then, the magnetic field at O is-
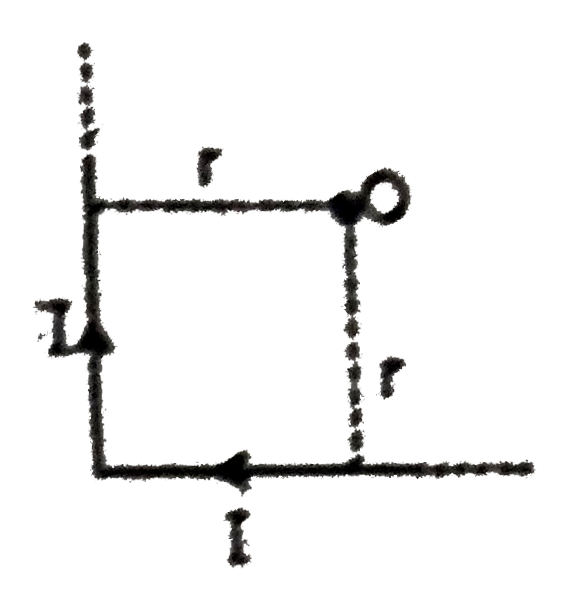 AzeroBμ0I/2πrCμ0I2πr(1+1√2)Dμ0I4πr(1+1√2)
AzeroBμ0I/2πrCμ0I2πr(1+1√2)Dμ0I4πr(1+1√2) - Question 2 - Select One
A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
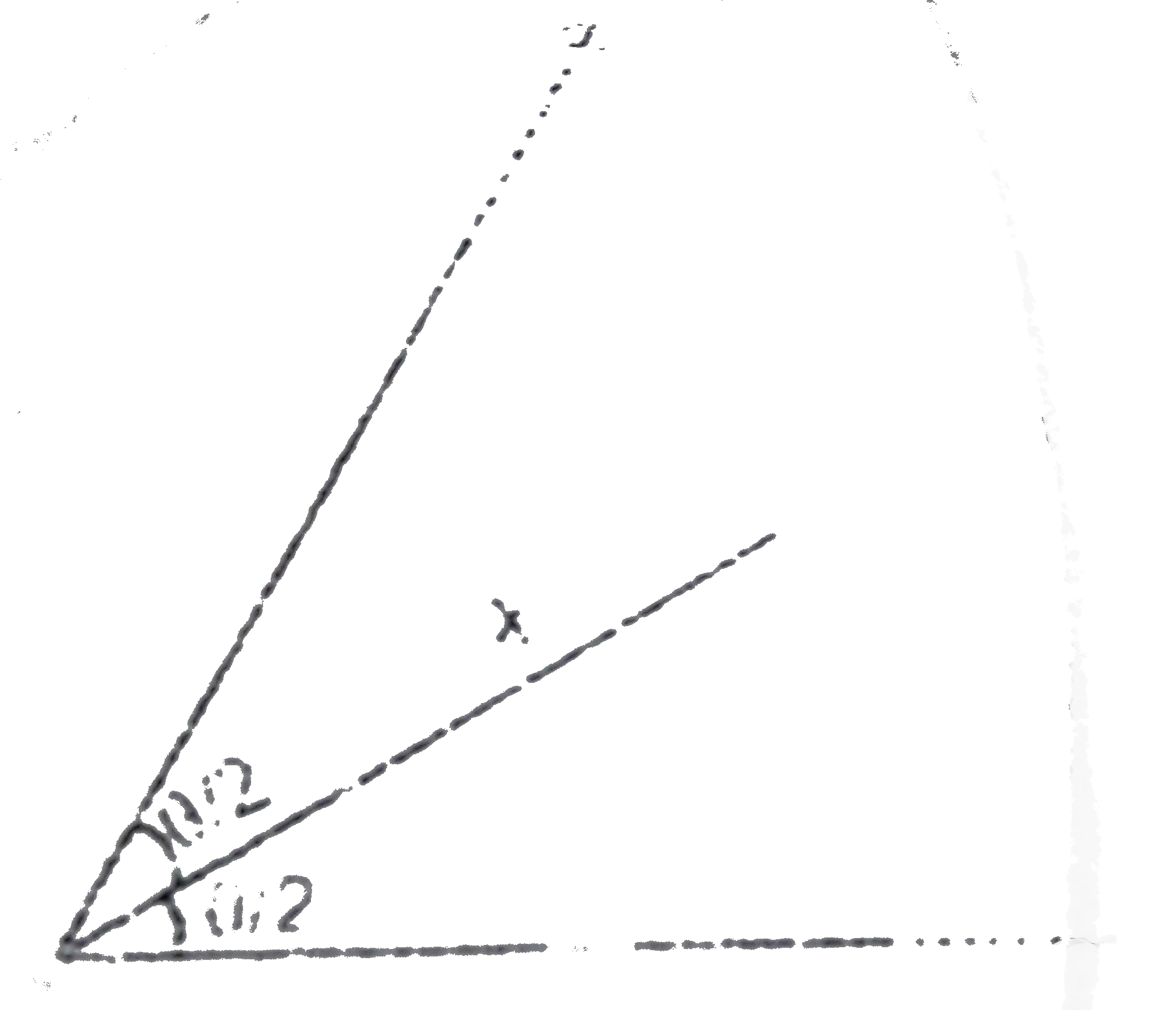 Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙
Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙ - Question 3 - Select One
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2)
Alongwirecarry∈gacurrentiisbent→formapla≠∠α. F∈dthemag≠ticfieldBatap∮onthebisec→rofthis∠situatedatadistancexomthevertex.
View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in
 View Solution
View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.
 View Solution
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
 View Solution
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View Solution

