A long current wire is bent in the shapes shown in figure. The circular portion has radius R. The magnetic induction at the center of the circular segment is

−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]
μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]
−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]
μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]
The correct Answer is:a
(a) Figure −(d) shows magnetic field lines of a long wire. Note the direction of magnetic induction at pointsP,Q,R and S. From right − hand thumb rule the magnetic fields at points P,Q,R and S lie along the unit vectors (ˆj),(−ˆk),(−ˆj) and (ˆk) respectively. 
Magnetic field due to segment ,AB,
−→B1=μ0I4πR(−ˆk)
Magnetic field due to circular segment BCD,
−→B2=μ0I2R×(π2π)(−ˆi)
Magnetic field due to segment DE,
−→B3=μ0I4πR(−ˆk)
Resultant magnetic field,
−→B3=−→B1+−→B2+−→B3 =−μ0I4πR[2ˆk+πˆj]
(b) Magnetic field due to segment AB,
−→B1=μ0I4πR(−ˆk)
Magnetic field due to circular segment BCD,
−→B2=μ0I2R(π2π)(−ˆi)
Magnetic field due to segment DE,
−→B3=μ0I4πr(−ˆk)
Resultant magnetic field
−→BR=−→B1+−→B2+−→B3=−μ0I4πR[ˆk+(π+1)ˆi]
(c) Magnetic field due to segment AB,
−→B1=μ0I4πR(−ˆk)
Magnetic field due to circular segment BCDE,
−→B2=μ0I2R×(3π/22π)(−ˆi)
Magnetic field due to segment EF,
−→B3=μ0I4πR×(−ˆj)
Resultant magnetic field.
−→BR=−→B1+−→B2+−→B3=−μ0I4πR[ˆk+ˆj+3π2ˆi]
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-VI (SINGLE ANSWER QUESTION)
81 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level =I (H.W)
42 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT Based Questions
20 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
A long straight wire carrying current I is bent into the shape as shown in the figure. The circular portion of the wire has radius (10/π)m. The centre of this circle is at a distance 1m from the straight portion of the wire. What is the magnitude of the magnetic field at the centre of the circular portion? Given π2=10.
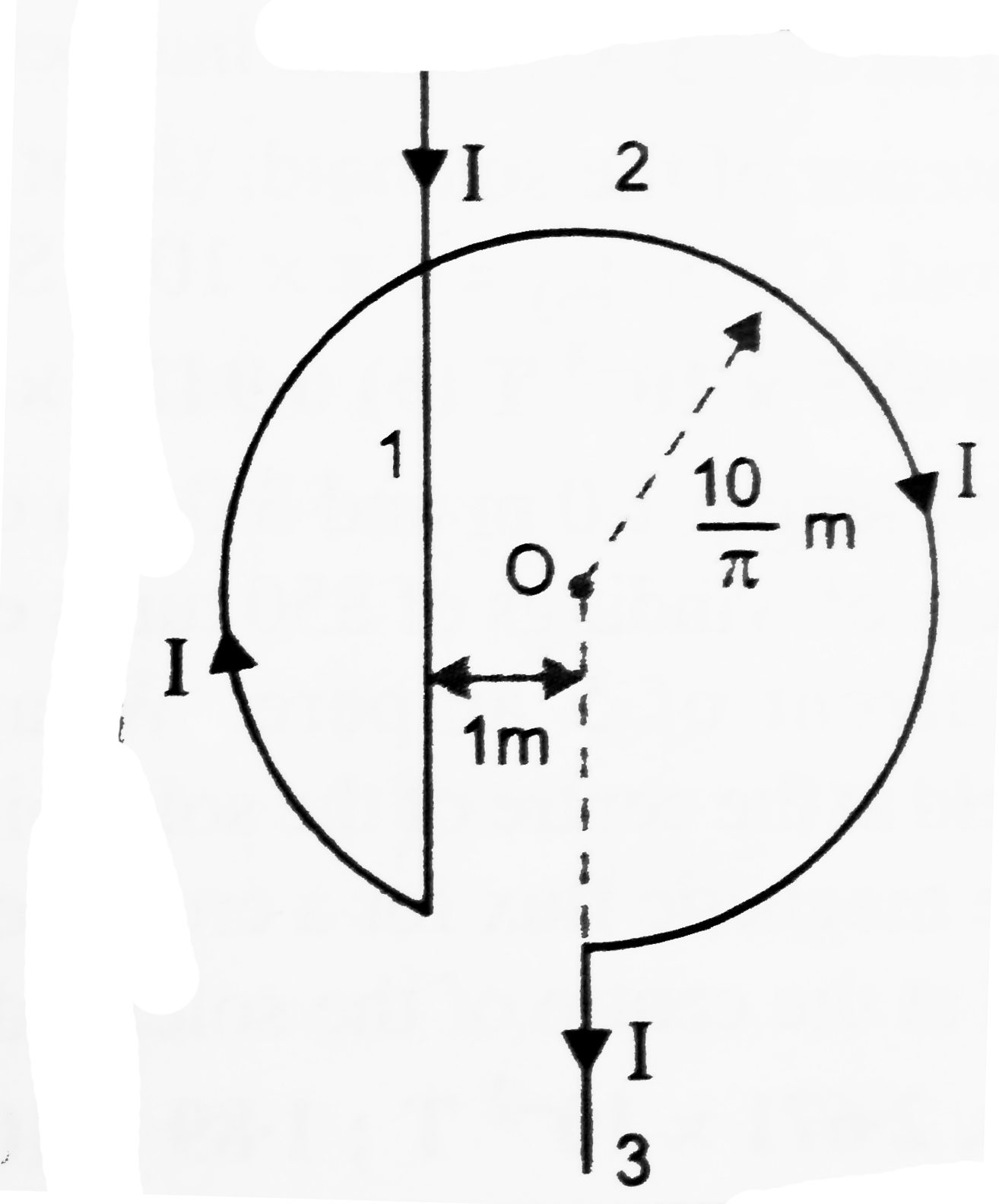
View SolutionA long wire is bent into the shape shown in the figure. Without cross-contact at P. Determine the magnitude and direction of B at the center of the circular portion of radius R when a current I flows as indicated.
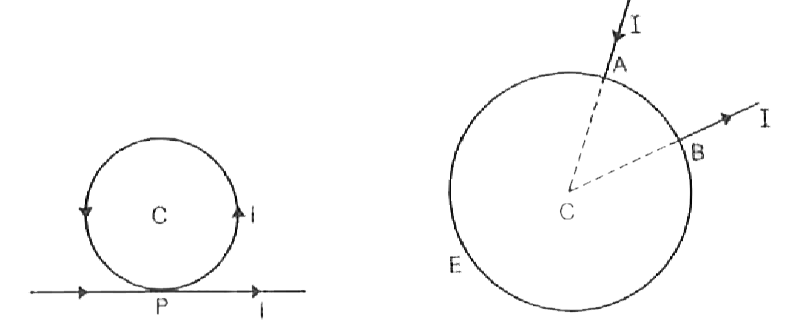
View Solution
Knowledge Check
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2An infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is
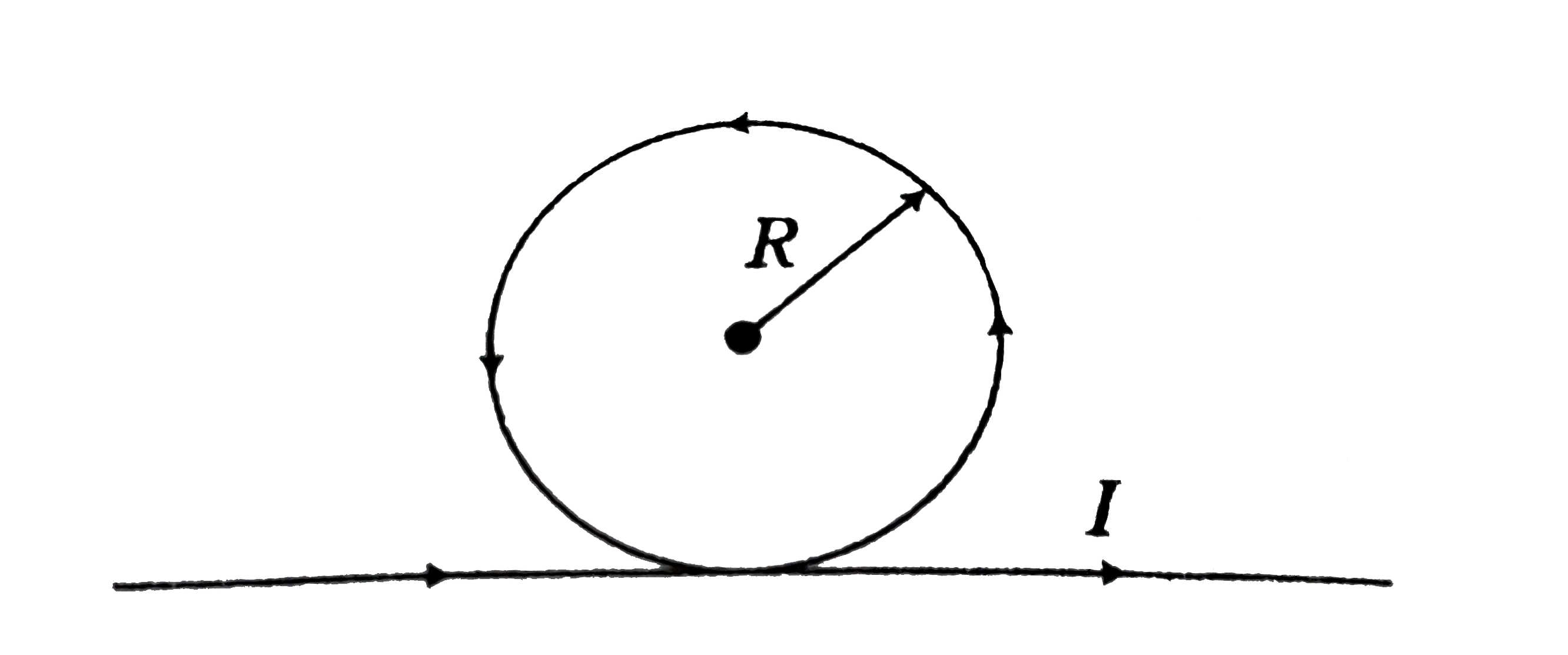 AZeroBinfinityCμ04π2ir(π+1)TeslaDμ04π2ir(π−1)Tesla
AZeroBinfinityCμ04π2ir(π+1)TeslaDμ04π2ir(π−1)TeslaAn infinitely long straight conductor is bent into the shape as shown in the figure. It carries a current of i ampere and the radius of the circular loop is V metre. The magnetic induction at the centre of the circular part is-
 Aμ0I4π(π−1)Bμ0i2a(1−1π)Cμ0i2a(π−1)Dμ0i4a(1−1π)
Aμ0I4π(π−1)Bμ0i2a(1−1π)Cμ0i2a(π−1)Dμ0i4a(1−1π)
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R meter. The magnetic induction at the centre of loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View Solution
