A thin semicircular conducting ring of radius R is falling with its plane verticle in a horizontal magnetic inducting B. At the position MNQ, the speed of the ring is V and the potential difference developed across the ring is

zero
BVπR2/V and M is at higher potential
πRBV and Q is at higher potential
2RBV and Q is at higher potential
The correct Answer is:D
Step by step video, text & image solution for A thin semicircular conducting ring of radius R is falling with its plane verticle in a horizontal magnetic inducting B. At the position MNQ, the speed of the ring is V and the potential difference developed across the ring is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (C.W)28videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level - III64videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Assertion & Reason11videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -443videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)14videos
ELECTRO MAGNETIC WAVES
Similar Questions
A thin semicircular conducting ring of radius R is falling with its plane vertical in a horizontal magnetic induction B. At the position MNQ shown in the fig, the speed of the ring is V. The potential difference developed across the semicircular ring is
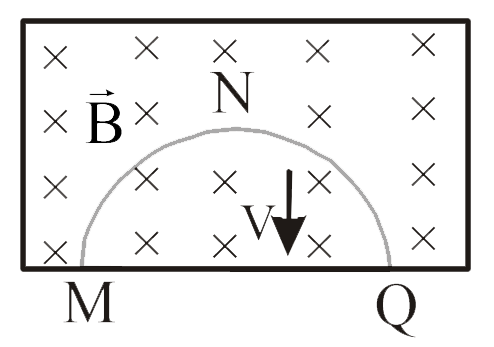 View Solution
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A thin semi-circular conducting ring of radius R is falling with its plane verticle in horizontal magnetic induction (→B). At the position MNQ the speed of the ring is v, and the potential difference developed across the ring is
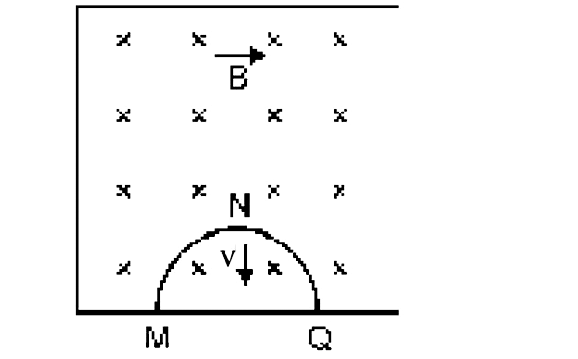 AzeroBBvπR2/2 and M is higher potencialCπ RBv ans Q is at higher potentialD2RBv ans Q is at higher potential
AzeroBBvπR2/2 and M is higher potencialCπ RBv ans Q is at higher potentialD2RBv ans Q is at higher potential - Question 2 - Select One
A thin circular -conducting ring having N turns of radius R is falling with its plane vertical in a horizontal magnetic field B . At the position MNQ the speed of ring is v the induced e.m.f developed across the ring is
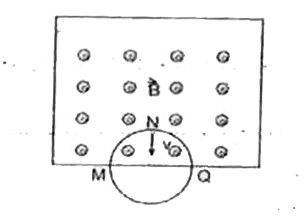 AZeroBBvπR2N2 and M is at higher potentialCNπ BRv and Q is at higher potentialD2RBvN and Q is at lower potential
AZeroBBvπR2N2 and M is at higher potentialCNπ BRv and Q is at higher potentialD2RBvN and Q is at lower potential - Question 3 - Select One
A thin semicircuilar conducting ring (PQR) of radius r is falling with its plane vertical in a horizontal magnetic field B, as shown in Fig. The potential difference developed across the ring when its speed is υ, is
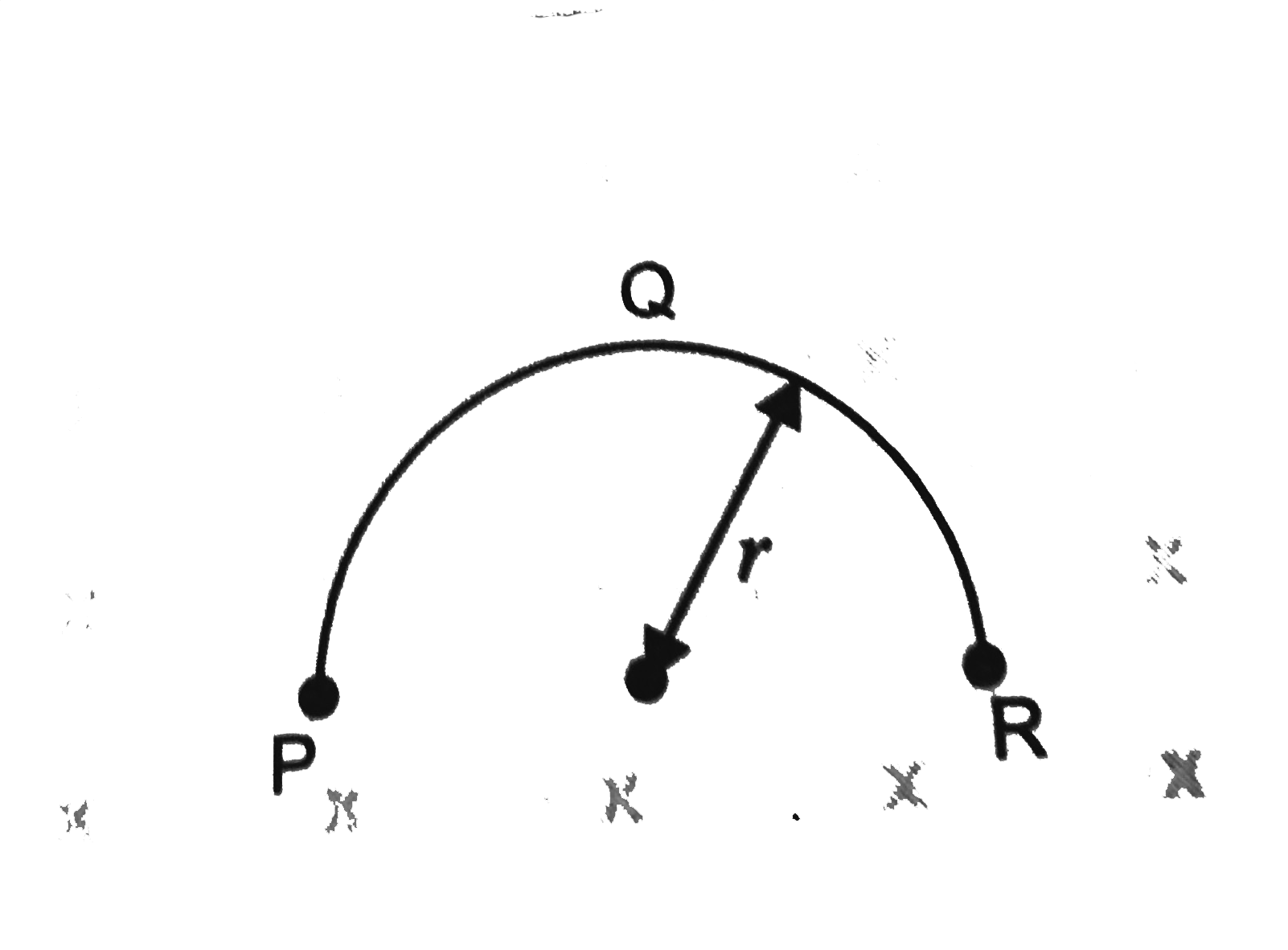 AzeroBBυπr2 and P is at higher potentialCπrBυ and R is at higher potentialD2rBυ and R is at higher potential
AzeroBBυπr2 and P is at higher potentialCπrBυ and R is at higher potentialD2rBυ and R is at higher potential
A vertical conducting ring ogradius R falls vertically in a horizontal magnetic field of magnitude B. The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v,
 View Solution
View SolutionA vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
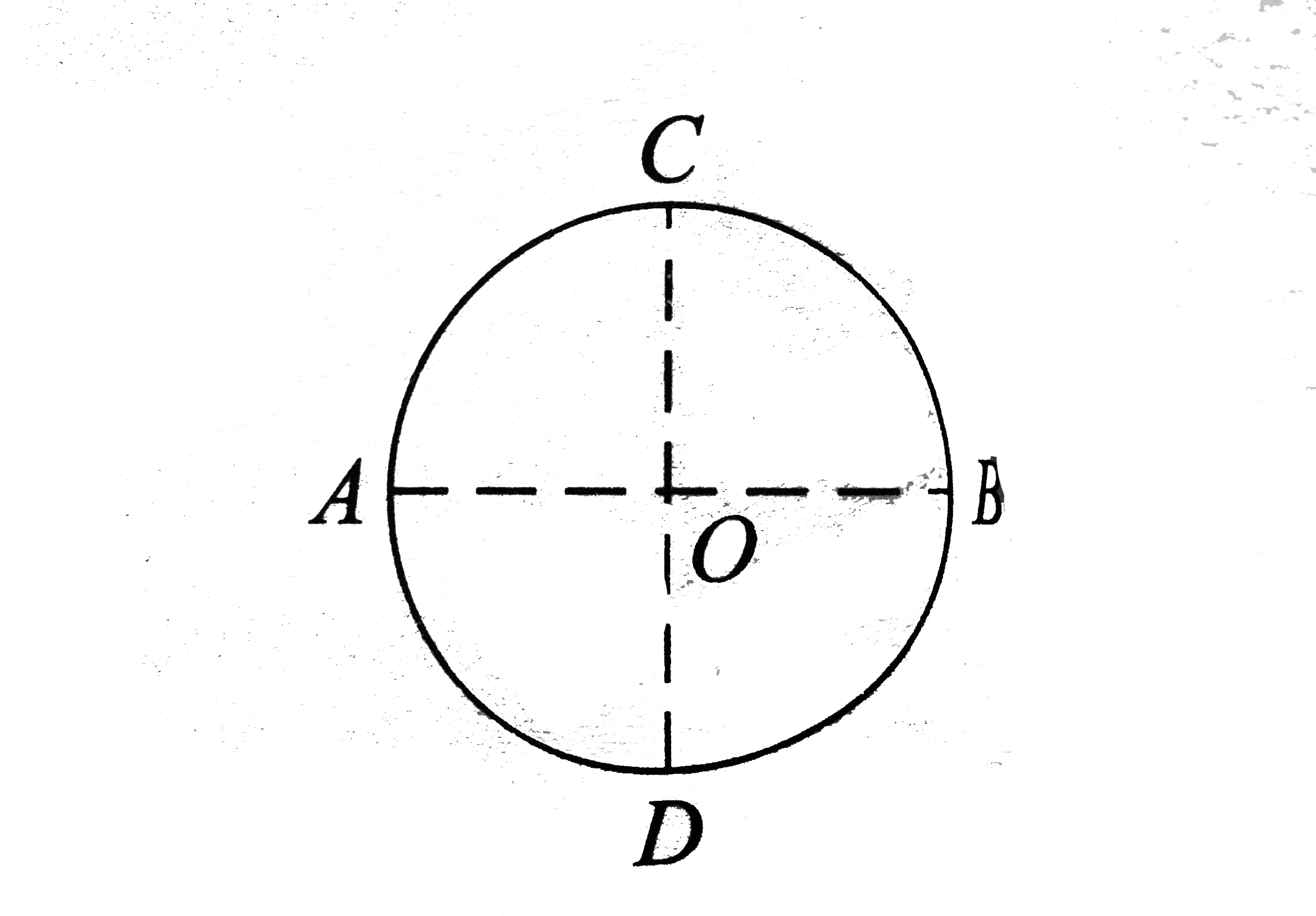 View Solution
View SolutionA vertical conduction ring of radius R falls vertically in a horizontal magnetic field of magnitude B with constant speed v . The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v , (i) A and D are at different potential
(ii) A and D are at the same potential
(iii) C and E are at the same potential
(iv) The potential difference between A and D is 2BRv , with D a higher potential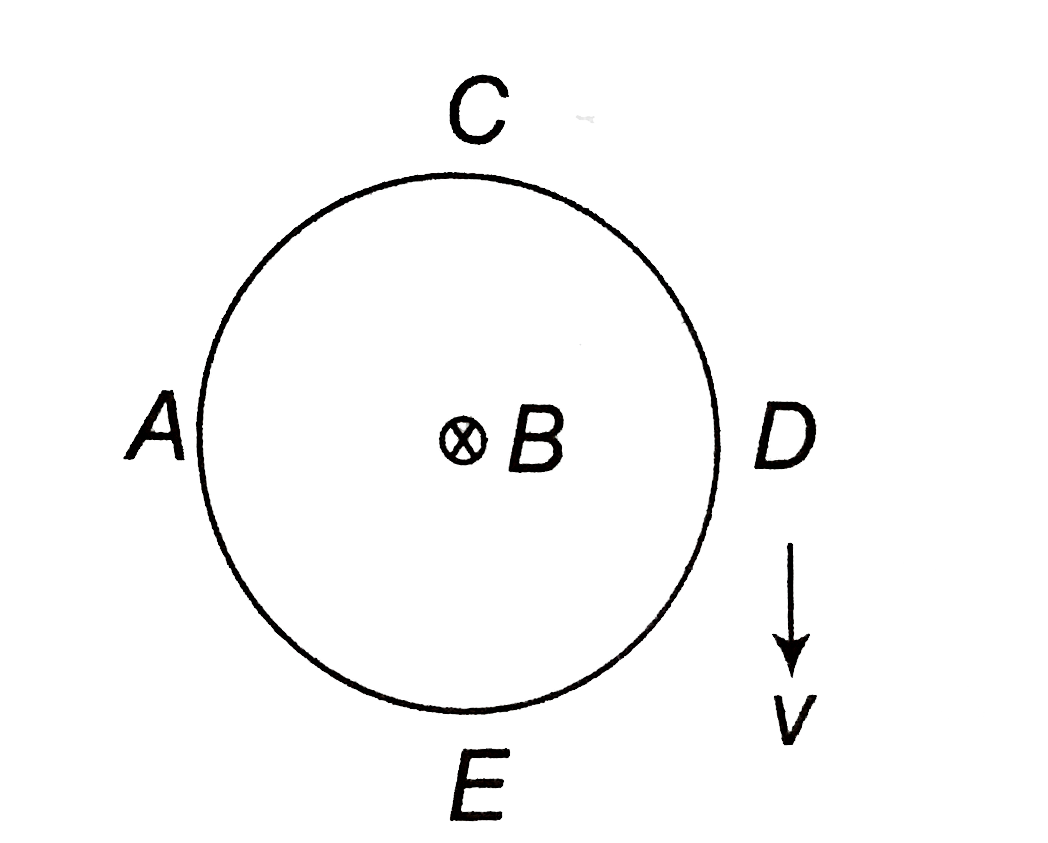 View Solution
View Solution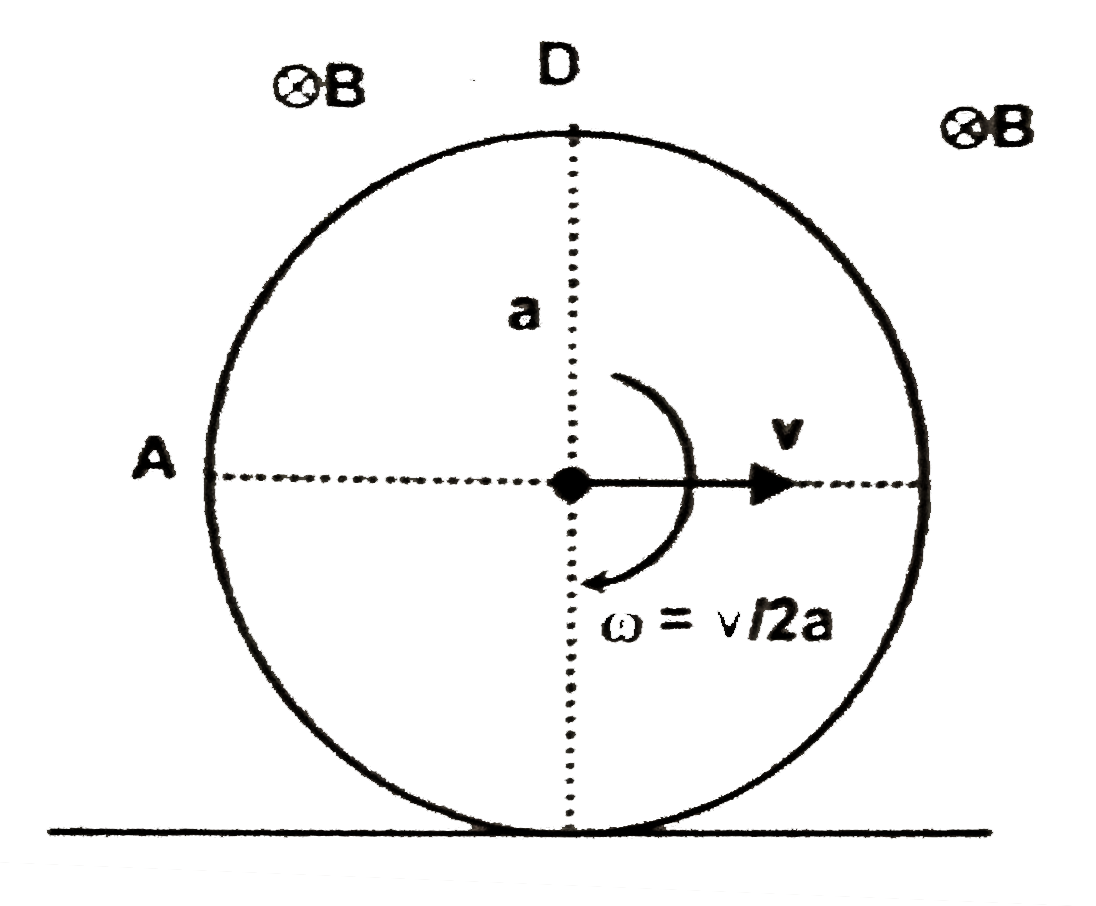
A circular conducting ring of radius 'a' is rolling with slipping on a horizontal surface as shown. A uniform magnetic field B is existing perpendicular to the plane of motion of the ring. The emf iniduced between the points A and D of the ring isView SolutionA semi circular conducting ring acb of radius R moves with constant speed v in a plane perpendicular to uniform magnetic field B as shown in figure.
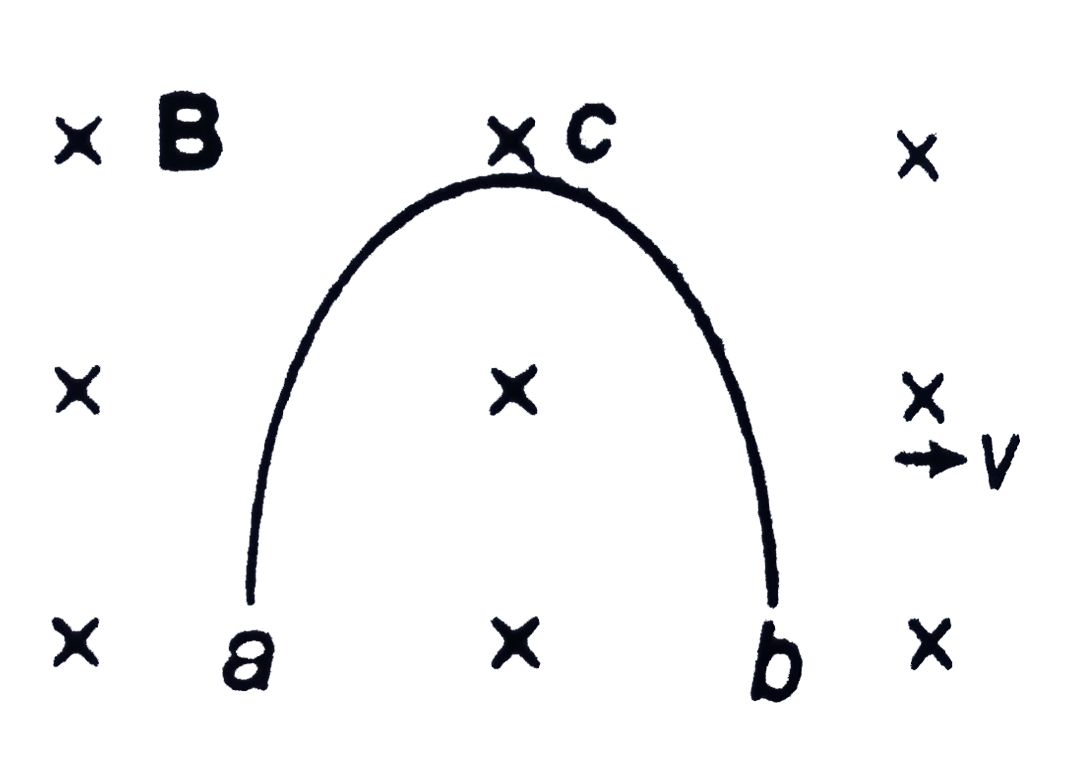
Identify the correct statement.View Solution

