A flexible wire loop in the shape of a circle has a radius that grows linearly with time. There is a magnetic field perpendicular to the plane of the loop that has a magnitude inversely proportional to the distance from the centre of the loop, B(r)∝1r How does the emf E vary with time?
E∝t2
E∝t
E∝√t
E is constant
The correct Answer is:D
Let radius of the loop r at time t and in further time dt, radius increases by dr.
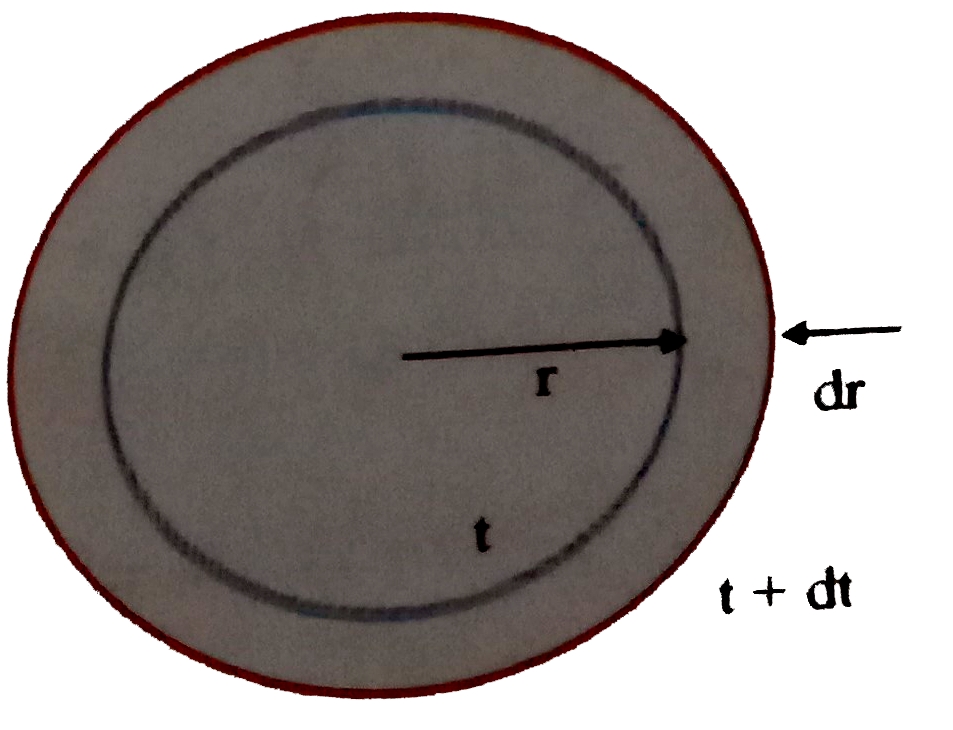
The change in flux: dϕ=(2πdr)B
⇒e=dϕdt=2πr(drdt)kr
⇒e=2πck(constant)[∴drdt=c,B=kr]
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-I(H.W)
23 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -4
43 Videos
- ELECTRO MAGNETIC WAVESBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)
14 Videos
Similar Questions
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
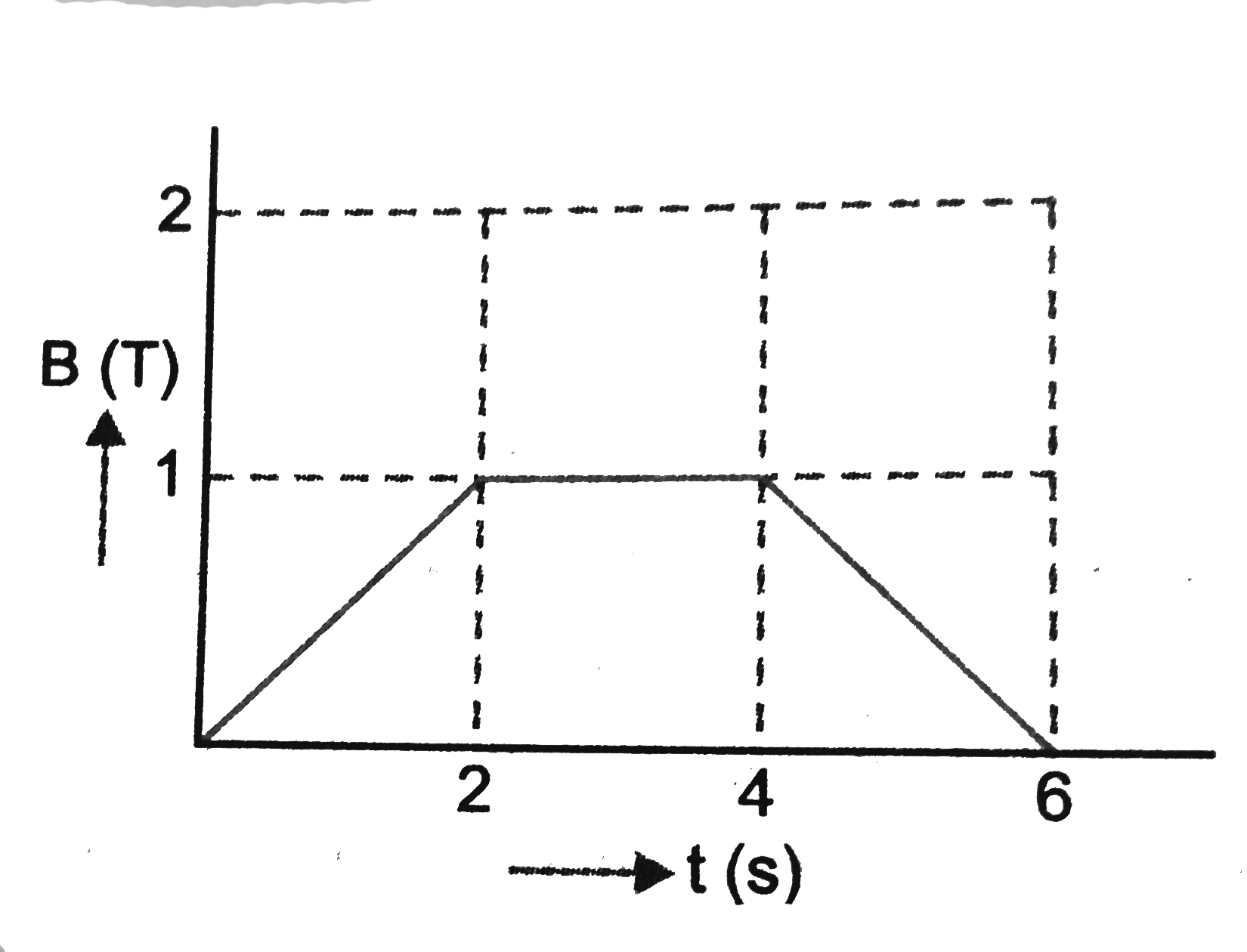
View SolutionThe magnetic field through a circular loop of wire 12 cm in radius and 8.5 ohm resistance, changes with time as shown in Fig. The magnetic field is perpendicular to the plane of the loop. Calculate the induced current in the loop and plot is as a function of time.
View Solution
Knowledge Check
A conducting circular loop of radius r carries a constant i. It is placed in a uniform magnetic field B such that B is perpendiclar to the plane of thre loop is .What is the magnetic force acting on the loop?
AirBB2πirBCzeroDπirBA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
 A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzeroA conducting circular loop of radius r carries a constant current i.It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
AI r BB2πrIBCzeroDπrIB
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is

View SolutionThe graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conductig loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude fo the emf induced in the loop, greater first

View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field→B such that vecB is perpendicular to the plane of the loop. What is the torque acting on the loop?
View Solution
