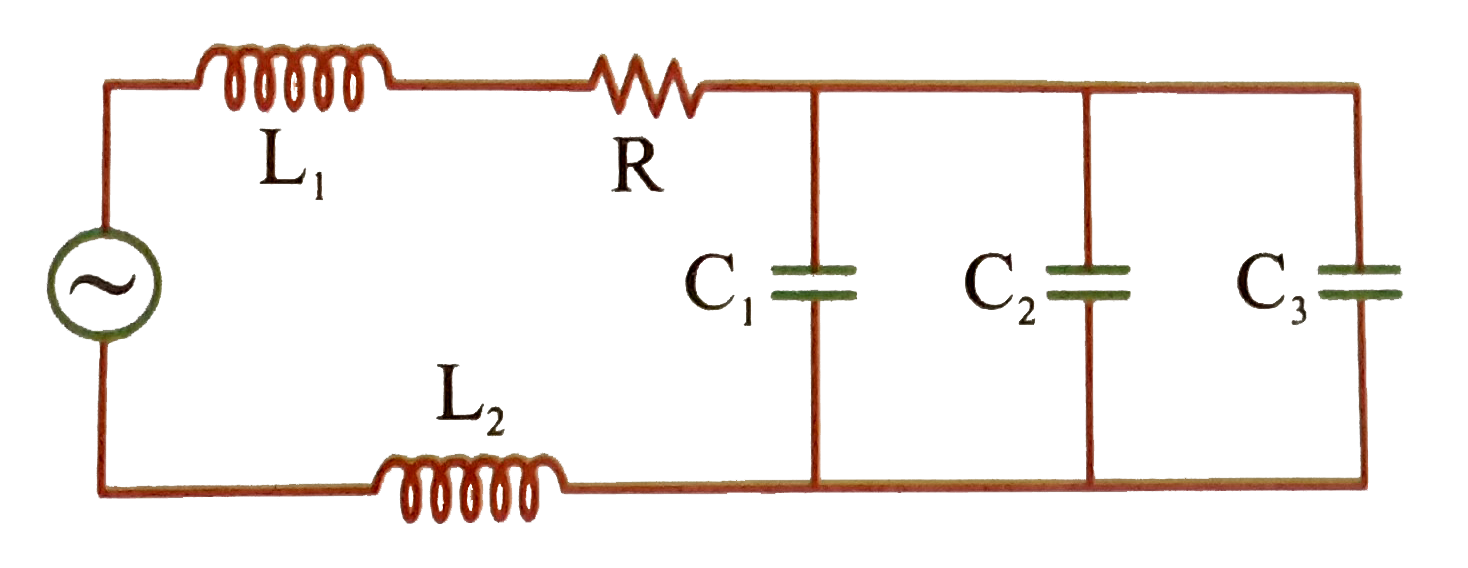
A generator with an adjustable frequency of oscillaton is connected to resistance, $R = 1000 Ω$ , inductance, $L_{1} = 1.7 m H$ and $L_{2} = 2.3 m H$ and capacitance, $C_{1} = 4 μ F, C_{2} = 2.5 μ F$ and $C_{3} = 3.5 μ F$ . The resonant angular frequency of the circuit is

A

$0.5 rad / s$

B

$0.5 \times 10^{4} rad / s$

C

$2 rad / s$

D

$2 \times 10^{- 4} rad / s$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$C_{eff} = C_{1} + C_{2} + C_{3}$
$= 4 μ F + 2.5 μ F + 3.5 μ F = 10 μ F$
$L_{eff} = L_{1} + L_{2} = 1.7 m H + 2.3 m H = 4 m H$
Resonance frequency,
$ω = \frac{1}{\sqrt{L_{eff} C_{eff}}} = \frac{1}{\sqrt{4 \times 10^{- 3} \times 10 \times 10^{- 6}}}$
$\frac{10^{4}}{2} = 0.5 \times 10^{4} rad / s$

|

Updated on:21/07/2023

Class 12 PHYSICS ALTERNATING CURRENT

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If resistance R $= 10 Ω$ , inductance L = 2 mH and capacitance $C = 5 μ F$ are connected in series to an AC source of frequency 50 Hz, then at resonance the impedance of circuit is
AZero
B $10 Ω$
C $1000 Ω$
D $10 K Ω$
Question 2 - Select One
When $L = 2 H, C = 32 μ F$ and $R = 10 Ω$ , then the resonant frequency is:
A $125 r a d s^{- 1}$
B $140 r a d s^{- 1}$
C $130 r a d s^{1}$
D $135 r a d s^{- 1}$
Question 3 - Select One
Find the time constant (in $μ s$ ) for the given RC circuits in the given order respectively.

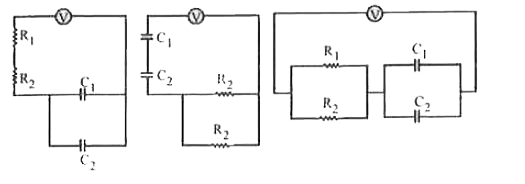
$R_{1} = 1 ω, R_{2} = 2 ω, C_{1} = 4 μ F, C_{2} = 2 μ F$
A $18, 4, \frac{8}{9}$
B $18, \frac{8}{9}, 4$
C $4, 18, \frac{8}{9}$
D $4, \frac{8}{9}, 18$

NARAYNA-ALTERNATING CURRENT-LEVEL - V

Home
Ask Doubt
Profile