If various elements, i.e., resistance capacitance and inductance which are in series and having values 1000Ω,1μF and 2.0H respectively. Given emf as, V=100√2sin1000t volts
Voltage across the resistor is
70.7 Volts
100 Volts
141.4 Volts
270.7 Volts
The correct Answer is:A
rms value of voltage across the source
Vrms=100√2√2=100 volt
From question, ω=1000rad/s
irms=Vrms|Z|=Vrms√R2+(XL−XC)2
=Vrms√R2+(ωL−1ωC)2
=100√(1000)2+(1000×2−11000x1×10−6)2
= 0.0707 amp
Since the current will be same every where in the circuit, therefore
P.D acrossresistor
VR=irmsR=0.0707×1000=70.7 volts
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ALTERNATING CURRENTEXERCISE - LEVEL - I (H.W)23videos
ALTERNATING CURRENT
- BOOK - NARAYNACHAPTER - ALTERNATING CURRENTEXERCISE - LEVEL - II(H.W)13videos
ALTERNATING CURRENT
- BOOK - NARAYNACHAPTER - ALTERNATING CURRENTEXERCISE - LEVEL - V83videos
ALTERNATING CURRENT
- BOOK - NARAYNACHAPTER - ATOMIC PHYSICSEXERCISE - LEVEL-II (H.W)14videos
ATOMIC PHYSICS
Similar Questions
Find the voltage across the various elements, i.e., resistance, capacitance and inductance which are in series and having values 1000Ω,1μF and 2.0 H respectively . Given emf as,
V = 100sqrt2 sin 1000 t VView SolutionFind the voltage across the various elements, i.e., resistance, capacitance and inductance which are in series and having values 100Ω,1μF and 2.0H, respectively. Given emf is
V=100√2sin1000t voltView Solution
Knowledge Check
- Question 1 - Select One
If various elements, i.e., resistance capacitance and inductance which are in series and having values 1000Ω,1μF and 2.0H respectively. Given emf as, V=100√2sin1000t volts
voltage across the inductor isA70.7 VoltsB101 VoltsC141.4 VoltsD270.7 Volts - Question 2 - Select One
If various elements, i.e., resistance capacitance and inductance which are in series and having values 1000Ω,1μF and 2.0H respectively. Given emf as, V=100√2sin1000t volts
voltages across the capacitor isA70.7 VoltsB102 VoltsC141.4 VoltsD270.7 Volts - Question 3 - Select One
A 100Ω resistance is connected in series with a 4H inductor. The voltage across the resistor is VR=2sin(1000t)V. The voltage across the inductors is
A80sin(1000t+π2)B40sin(1000t+π2)C80sin(1000t−π2)D40sin(1000π−π2)
Find the potential difference across resistance, capacitance and inductance in series LCR circuit where L=2.0H,C=1μFandR=100Ω. The applied emf has the form V=100√2sin(1000t)
View SolutionIn the series L−C−R circuit shown in the figure, the rms voltage across the resistor and inductor are 400 V and 700 V respectively. If the applied voltage is E=500√2sin(ωt), then the peak voltage across the capacitor is
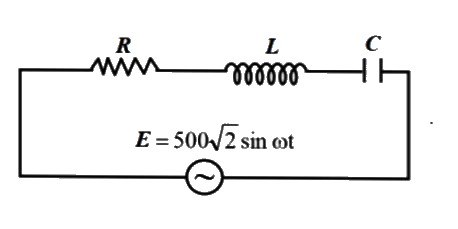 View Solution
View SolutionA series LCR circuit having resistance R, capacitance C and inductance L has a voltage source of angular frequency ω and voltage V∈. Output voltage (Vout) is taken as voltage across the resistor and inductor combined.
(a) Find η=VoutVin
(b) Find η in the limit of large ω(ω>>1RC,1√LC,RL)
(C )Find η in the limit of smallω(ω>>1RC,1√LC,RL)
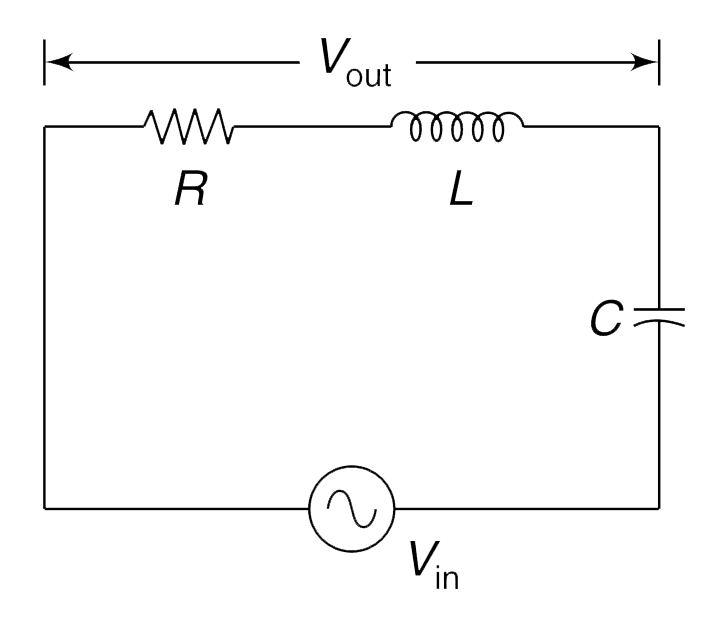 View Solution
View SolutionA resistor of 500Ω and an inductance of 0.5 H are in series with an ac source which is given by V=100√2sin(1000t). The power factor of the combination is
View SolutionAn alternating e.m.f. of 0.1 V is applied across an LCR series circuit having R=2Ω,C=40μFandL=100mH. At resonance, the voltage drop across the inductor is
View Solution

