A manufacturer produces three products x, y, z which he sells in two markets. Annual sales are indicated below:
Market Products
I 10.000 2.000 18.000
II 6.000 20.000 8.000
(a) If unit sale prices of x, y and z are Rs 2.50, Rs 1.50 and Rs 1.00, respectively, find the total revenue in each market with the help of matrix algebra.(b) If the unit costs of the above three commodities are Rs 2.00, Rs 1.00 and 50paise respectively. Find the gross profit.
To solve the problem step by step, we will break it down into two parts as per the question.
Part (a): Finding Total Revenue in Each Market
1. Define the Annual Sales Matrix (A):
The annual sales of products X, Y, and Z in two markets can be represented as a matrix A:
A=[100002000180006000200008000]
2. Define the Unit Sale Prices Matrix (B):
The unit sale prices of products X, Y, and Z can be represented as a matrix B:
B=⎡⎢⎣2.501.501.00⎤⎥⎦
3. Calculate Total Revenue (R):
The total revenue can be calculated by multiplying the sales matrix A by the prices matrix B:
R=A⋅B
Performing the matrix multiplication:
R=[100002000180006000200008000]⋅⎡⎢⎣2.501.501.00⎤⎥⎦
For the first market:
R1=(10000×2.50)+(2000×1.50)+(18000×1.00)=25000+3000+18000=46000
For the second market:
R2=(6000×2.50)+(20000×1.50)+(8000×1.00)=15000+30000+8000=53000
Thus, the total revenue matrix R is:
R=[4600053000]
Part (b): Finding Gross Profit
1. Define the Cost Price Matrix (C):
The unit costs of products X, Y, and Z can be represented as a matrix C:
C=⎡⎢⎣2.001.000.50⎤⎥⎦
2. Calculate Total Cost (T):
The total cost can be calculated by multiplying the sales matrix A by the cost price matrix C:
T=A⋅C
Performing the matrix multiplication:
T=[100002000180006000200008000]⋅⎡⎢⎣2.001.000.50⎤⎥⎦
For the first market:
T1=(10000×2.00)+(2000×1.00)+(18000×0.50)=20000+2000+9000=31000
For the second market:
T2=(6000×2.00)+(20000×1.00)+(8000×0.50)=12000+20000+4000=36000
Thus, the total cost matrix T is:
T=[3100036000]
3. Calculate Gross Profit (G):
The gross profit can be calculated by subtracting the total cost from the total revenue:
G=R−T
For the first market:
G1=R1−T1=46000−31000=15000
For the second market:
G2=R2−T2=53000−36000=17000
Thus, the gross profit matrix G is:
G=[1500017000]
Final Results:
- Total Revenue in Market I: Rs 46000
- Total Revenue in Market II: Rs 53000
- Gross Profit in Market I: Rs 15000
- Gross Profit in Market II: Rs 17000
---
The annual sales of products X, Y, and Z in two markets can be represented as a matrix A:
A=[100002000180006000200008000]
The unit sale prices of products X, Y, and Z can be represented as a matrix B:
B=⎡⎢⎣2.501.501.00⎤⎥⎦
The total revenue can be calculated by multiplying the sales matrix A by the prices matrix B:
R=A⋅B
R=[100002000180006000200008000]⋅⎡⎢⎣2.501.501.00⎤⎥⎦
R1=(10000×2.50)+(2000×1.50)+(18000×1.00)=25000+3000+18000=46000
R2=(6000×2.50)+(20000×1.50)+(8000×1.00)=15000+30000+8000=53000
R=[4600053000]
The unit costs of products X, Y, and Z can be represented as a matrix C:
C=⎡⎢⎣2.001.000.50⎤⎥⎦
The total cost can be calculated by multiplying the sales matrix A by the cost price matrix C:
T=A⋅C
T=[100002000180006000200008000]⋅⎡⎢⎣2.001.000.50⎤⎥⎦
T1=(10000×2.00)+(2000×1.00)+(18000×0.50)=20000+2000+9000=31000
T2=(6000×2.00)+(20000×1.00)+(8000×0.50)=12000+20000+4000=36000
T=[3100036000]
The gross profit can be calculated by subtracting the total cost from the total revenue:
G=R−T
G1=R1−T1=46000−31000=15000
G2=R2−T2=53000−36000=17000
G=[1500017000]
- Total Revenue in Market I: Rs 46000
- Total Revenue in Market II: Rs 53000
- Gross Profit in Market I: Rs 15000
- Gross Profit in Market II: Rs 17000
Similar Questions
A manufacturer produces three products x,y,z which he sells in two markets ,Annual sales are indicated below:
MarketproductsI10,0002,00018,000II6,00020,0008,000
(A) if unit sale prices of x,y and z are Rs. 2.50, Rs. 1.50 and Rs. 1.00, respectively , find the total revenue algebra .
(b) if the unit costs of the above three commodities are Rs. 2.00,Rs. 1.00 and 50 paise respectively, find the gross profit.
View SolutionA manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below

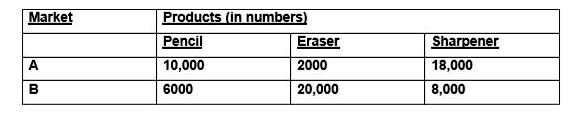
If the unit Sale price of Pencil, Eraser and Sharpener are Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively, and unit cost of the above three commodities are Rs. 2.00, Rs. 1.00 and Rs. 0.50 respectively, then,
Based on the above information answer the following:
Total revenue of market B
View Solution
Knowledge Check
A marketing agent earns a commission of 2% on first Rs. 2,00,000, 1.5% on next Rs 2,00,000 and 1% on the remaining amount of sales made in a month. If the sales achieved by the agent for the month of April 2018 are Rs. 5,68,000. The commission earned is
किसी विपणन एजेंट को एक माह में पहले 2,00,000 रुपये की बिक्री पर 2%, अगले 200000 रुपये की बिक्री पर 1.5% तथा बिक्री की शेष राशि पर 1% कमीशन मिलता है | यदि अप्रैल 2018 माह में उस एजेंट ने 5,68,000 रुपये की बिक्री की है, तो उसके द्वारा प्राप्त कमीशन ज्ञात करें |ARs 8,680BRs 7,730CRs 8,240DRs 7,105
A manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below

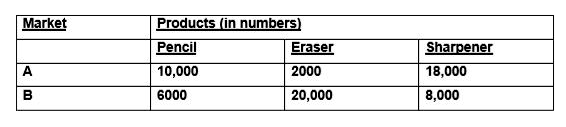
If the unit Sale price of Pencil, Eraser and Sharpener are Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively, and unit cost of the above three commodities are Rs. 2.00, Rs. 1.00 and Rs. 0.50 respectively, then,
Based on the above information answer the following:
Total revenue of market A
View SolutionA manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below

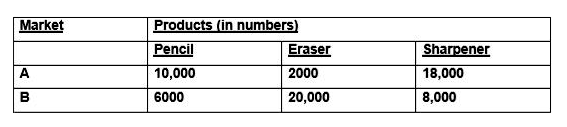
If the unit Sale price of Pencil, Eraser and Sharpener are Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively, and unit cost of the above three commodities are Rs. 2.00, Rs. 1.00 and Rs. 0.50 respectively, then,
Based on the above information answer the following:
Profit in market A and B respectively are
View SolutionA manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below

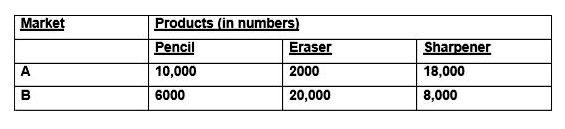
If the unit Sale price of Pencil, Eraser and Sharpener are Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively, and unit cost of the above three commodities are Rs. 2.00, Rs. 1.00 and Rs. 0.50 respectively, then,
Based on the above information answer the following:
Cost incurred in market A
View SolutionA manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets. Annual sales are indicated below

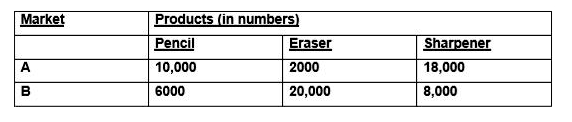
If the unit Sale price of Pencil, Eraser and Sharpener are Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively, and unit cost of the above three commodities are Rs. 2.00, Rs. 1.00 and Rs. 0.50 respectively, then,
Based on the above information answer the following:
Gross profit in both market
View SolutionThe cost of a car is Rs. 3,00,000. The cost of a motorbike is Rs. 50,000. The ratio of the cost of motorbike to the cost of car is
View SolutionIf total assets of a business are Rs. 2,00,000 and net worth (Capital ) is Rs. 1,50,000, Calculate Creditors.
View SolutionA firm sells goods at Cost plus 25%. Sales to credit customers (3/4 of total) was Rs. 1,80,000.
His Opening and Closing Stocks were Rs. 20,000 and Rs. 15,000 respectively. Find out the value of Purchases.
View Solution
