Let and be two planes. Then, which of the following statement(s) is (are) TRUE? The line of intersection of and has direction ratios (b) The line is perpendicular to the line of intersection of and (c) The acute angle between and is (d) If is the plane passing through the point and perpendicular to the line of intersection of and , then the distance of the point from the plane is
Step by step video & image solution for Let P_1:2x+y-z=3 and P_2: x+2y+z=2 be two planes. Then, which of the following statement(s) is (are) TRUE? The line of intersection of P_1 and P_2 has direction ratios 1,\ 2,\ -1 (b) The line (3x-4)/9=(1-3y)/9=z/3 is perpendicular to the line of intersection of P_1 and P_2 (c) The acute angle between P_1 and P_2 is 60o (d) If P_3 is the plane passing through the point (4,\ 2,\ -2) and perpendicular to the line of intersection of P_1 and P_2 , then the distance of the point (2,\ 1,\ 1) from the plane P_3 is 2/(sqrt(3)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Find an equation or the line that passes through the point P(2, 3, 1) and is parallel to the line of intersection o the planes x+2y−3z=4 and x−2y+z=0 .
View SolutionFind the equation of the line passing through the point P(4,6,2) and the point of intersection of the line x−13=y2=z+17and the plane x + y - z = 8 .
View Solution
Knowledge Check
- Question 1 - Select One
A plane P = 0 passing through the point (1, 1, 1) is perpendicular to the planes 2x−y+2z=5 and 3x+6y−2z=7. If the distance of the point (1, 2, 3) from the plane P = 0 is k units, then the value of 34k2 is equal to
A8√17B16C64D128 - Question 2 - Select One
Let P1:x−2y+3z=5andP2:2x−3y+z+4=0 be two planes. The equation of the plane perpendicular to the line of intersection to the line of intersection of P1=0 and P2= and passing through (1,1,1) is
A11x−5y+7z−13=0B7x+5y+z=13Cx+2y+z−4=0Dx−2t+4z+3=0 - Question 3 - Select One
P1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2

The angle between P1andP2 is ________.Acos−1(15)Bcos−1(1√55)Ccos−1(2√11)Dcos−1(3√11)
Let P be the plane passing through the point (0,1,–1) and perpendicular to the line of intersection of the planes 2x+z=3 and 3y+2z=5 . If plane P intersects x -axis, y -axis, z -axis, at points A,B,C respectively then area of triangle ABC equals
View SolutionP1:x+3y−z=0andP2,y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
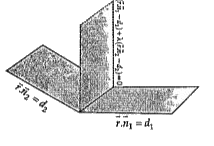
Equation of P3 isView SolutionA line is drawn from the point P(1,1,1)and perpendicular to a line with direction ratios, (1,1,1) to intersect the plane x+2y+3z=4 at Q. The locus of point Q is
View SolutionP1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
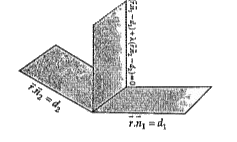
__________ is a point on P3.View SolutionP1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
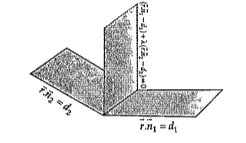
Distance of P3 from origin is _______ units.View Solution

