Find X and Y, if X+Y=[5209]and X−Y=[360−1].
To find the matrices X and Y given the equations X+Y=[5209] and X−Y=[360−1], we can follow these steps:
Step 1: Add the two equations
We start by adding the two equations:
(X+Y)+(X−Y)=[5209]+[360−1]
This simplifies to:
2X=[5+32+60+09−1]=[8808]
Step 2: Solve for X
Now, we can solve for X by dividing both sides by 2:
X=12[8808]=[4404]
Step 3: Subtract the two equations
Next, we subtract the second equation from the first:
(X+Y)−(X−Y)=[5209]−[360−1]
This simplifies to:
2Y=[5−32−60−09+1]=[2−4010]
Step 4: Solve for Y
Now, we can solve for Y by dividing both sides by 2:
Y=12[2−4010]=[1−205]
Final Result
Thus, we have:
X=[4404],Y=[1−205]
We start by adding the two equations:
(X+Y)+(X−Y)=[5209]+[360−1]
This simplifies to:
2X=[5+32+60+09−1]=[8808]
Now, we can solve for X by dividing both sides by 2:
X=12[8808]=[4404]
Next, we subtract the second equation from the first:
(X+Y)−(X−Y)=[5209]−[360−1]
This simplifies to:
2Y=[5−32−60−09+1]=[2−4010]
Now, we can solve for Y by dividing both sides by 2:
Y=12[2−4010]=[1−205]
Thus, we have:
X=[4404],Y=[1−205]
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - MATRICESEXERCISE - EXERCISE 3.110videos
MATRICES
- BOOK - NCERTCHAPTER - MATRICESEXERCISE - MISCELLANEOUS EXERCISE15videos
MATRICES
- BOOK - NCERTCHAPTER - MATRICESEXERCISE - EXERCISE 3.312videos
MATRICES
- BOOK - NCERTCHAPTER - LINEAR PROGRAMMINGEXERCISE - SOLVED EXAMPLES11videos
LINEAR PROGRAMMING
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 13.218videos
PROBABILITY
Similar Questions
The number of all possible matrices of order 3×3with each entry 0 or 1 is:
(a) 27 (b) 18 (c) 81 (d) 51201:20View SolutionFind x, if [x−5−1]⎡⎢⎣102021203⎤⎥⎦⎡⎢⎣x41⎤⎥⎦=O.
01:55View SolutionFind 12(A+A')and 12(A−A'), when A=⎡⎢⎣0ab−a0c−b−c0⎤⎥⎦
02:37View Solution(Transportation problem) There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below :
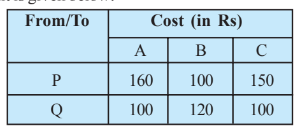
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?03:35View SolutionIf A and B are two events such that P(A)=12, P(B)=712and P(not A or not B) = 14. State whether A and B are independent?
02:17View SolutionIf (x)/(y)+(y)/(x)=-1,[x,y!=0], then find the value of x^(3)-y^(3)
01:17View Solution(x)/(y)+(y)/(x)=-1(where,x,y!=0) then find the value of x^(3)-y^(3)
02:15View SolutionFind the values of x,y,z from the following matrix equation : [x+yx+y+z2x+y0]=[3650]
03:19View SolutionIf X and Y are two matrices such that X+Y=[4−352]andX−Y=[6−532], then find the matrices X and Y.
02:29View SolutionX और Y ज्ञात कीजिए, यदि X+Y=[5209] तथा X−Y=[360−1] है।
03:35View Solutionनिम्नलिखित आव्यूह समीकरण से x,y,z के मान ज्ञात कीजिए -
[x+yx+y+z2x+y0]=[3650].02:58View Solutionयदि X+Y =[5009] तथा X−Y=[360−1]है तो X तथा Y ज्ञात कीजिए ।
10:35View SolutionIf (3,6) is the vertex and (4,5) is the focus of a parabola then the equation of its directrix is
A) x+y+5=0 B) x+y-5=0
C) x-y-5=0 D) x-y+5=002:42View SolutionFind matrices X and Y if : X+Y=[5209] and X−Y=[360−1].
04:29View SolutionIf X+Y=[5209] and X−Y=[360−1],<br>find 2X-3Y.
03:42View SolutionFind x+y and x−y if x=[5209] and y=[360−1] .
01:40View Solution

