f(m)<0.f(x)=ax2−bx+c,m lies between the roots and f(m1)f(m2)<0, then one of the roots will lies between m1andm2
Step by step video & image solution for f(m)<0.f(x)=ax^2-bx+c,m lies between the roots and f(m_1)f(m_2)<0, then one of the roots will lies between m_1and m_2 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
If f(x) is a polynomial, show that between two roots of the polynomial equation f(x)=0, there lies at least one root of the polynomial f'(x)=0.
View SolutionFor the function f(x)=ax2+bx+c,a≠0 , the sum of the roots is equal to the product of the roots . Which could be f(x) ?
View SolutionIf f is defined in [1, 3] by f(x)=x3+bx2+ax such that f(1)−f(3)=0 and f'(c) =0 where c=2+1√3, then (a, b) =
View SolutionIf f(x) be a quadratic polynomial such that f(x)=0 has a root 3 and f(2)+f(−1)=0 then other root lies in
View SolutionLet f(x)=ax2+bx+c=0 be a quadratic equation and α,β are its roots then f(−x)=0 is an equation whose roots
View SolutionGravitational force between masses m1 and m2 is F. If a third mass m3 is placed near m1 and m2, then the force between m1 and m2 would be
View SolutionGravitational force between masses m_1 and m_2 is F. If a third mass m_3 is placed near m_2 and m_3 then the force between m_1 and m_2 would be
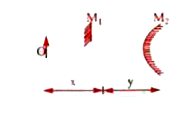
View SolutionAn object O is placed in front of a small plane mirror M1 and a large convex mirror M2 of focal length f. The distance between O and M1 is x and the distance between M1andM2 is y. The images of O formed by M1andM2 coincide. The magnitude of f is
View Solution
