ABCD is a cyclic quadrilateral such that ∠A=( 4y+20 )°, ∠B=( 3y−5 )°, ∠C=( −4x)° and ∠D=( -7x+5 )° . Find the four angles.
Sum of opposite angles=180∘
∠A+∠C=180∘
(4y+20)∘+(−4x)∘=180∘
−4x+4y=160∘
−x+y=40∘
−x=40−y
∠B+∠D=180∘
(3y−50)∘+(−7x+5)∘=180∘
−7x+3y=180∘
Put −x=40−y in −7x+3y=180∘
7(40−y)+3y=180∘
280−7y+3y=180∘
100=4y
y=25∘
−x=40−y
x=y−40
x=−15∘
Answer,
∠A=4y+20=100+20=120∘
∠B=(3y−5)∘=70∘
∠C=(−4x)∘=60∘
∠D=(−7x+5)∘=110∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD (taken in order) is a cyclic quadrilateral in which ∠A=(x+y+10)∘,∠B=(y+20)∘,∠C=(x+y−30)∘ and ∠D=(x+y)∘. Find the value of x and y.
Ax=40∘,y=60∘Bx=50∘,y=40∘Cx=20∘,y=80∘Dnone of these
In the figure, ABCD is a cyclic quadrilateral, AX and DY are tangents, XˆAB=44∘,YˆDC=57∘,andBˆDC=26∘. Find the angles of quadrilateral ABCD
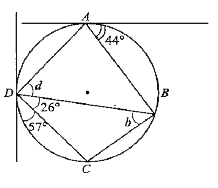 View Solution
View SolutionFind the angles of a cyclic quadrilateral ABCD in which ∠A=(4x+20)∘,∠B=(3x−5)∘,∠C=(4y)∘and∠D=(7y+5)∘.
View SolutionFind the four angles of a cyclic quadrilateral ABCD in which ∠A=(2x−1)o , ∠B=(y+5)o ∠C=(2y+15)o and ∠D=(4x−7)o .
View SolutionIn a given fig. ABCD is a cyclic quadrilateral with ∠BAD=100∘,∠ADC=85∘,∠ABC=x∘and∠DCB=y∘ Find x and y.
View SolutionIn a cyclic quadrilateral ABCD, ∠A=(2x+4)∘,∠B=(x+10)∘,∠C=(4y−4)∘ and ∠D=(5y+5)∘. Find the values of xandy hence find all the angles.
View SolutionFind the area of the quadrilateral ABCD whose vertices are A(1,0),B(5,3),C(2,7) and D(−2,4)
View SolutionThe angles of a cylic quadrilateral ABCD are ∠A=(2x+4)∘,∠B=(y+3)∘,∠C=(2y+10)∘,∠D=(4x−5)∘. Find x and y and hence the values of the four angles.
View Solution

