In Fig. 4.60, check whether AD is the bisector of ∠A of ABC in each of the following: (FIGURE) AB=6cm, AC=8cm, BD=1.5cm and CD=2cm (ii) AB=5cm, AC=12cm , BD=2.5cm and BC=9cm
Step by step video & image solution for In Fig. 4.60, check whether A D is the bisector of /_A of A B C in each of the following: (FIGURE) A B=6c m ,\ \ A C=8c m ,\ \ B D=1. 5 c m and C D=2c m (ii) A B=5c m ,\ \ A C=12 c m , B D=2. 5 c m and B C=9c m by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Fig. 4.60, check whether AD is the bisector of ∠A of ABC in each of the following: (FIGURE) AB=5cm, AC=10cm, BD=1.5cm and CD=3.5cm (ii) AB=4cm, AC=6cm, BD=1.6cm and CD=2.4cm (iii) AB=8cm, AC=24cm, BD=6cm and BC=24cm
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If AD=5.6cm , BC=6cm and BD=3.2cm , find AC . (ii) If AB=10cm , AC=6cm and BC=12cm , find BD and DC .
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=10.8cm, BD=4.5 cm, AC=4.8cm and AE=2.8cm (ii) AD=5.7cm, BD=9.5cm, AE=3.3cm and EC=5.5cm .
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=12 cm, AD=8 cm, AE=12 cm and AC=18 cm . (ii) AB=5.6 cm, AD=1.4 cm, AC=7.2 cm and AE=1.8 cm
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If BD=2.5cm, AB=5cm and AC=4.2cm , find DC . (ii) If BD=2cm, AB=5cm and DC=3cm, find AC . (iii) If AB=3.5cm , AC=4.2cm and DC=2.8cm , find BD .
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If AB=10cm , AC=14cm and BC=6cm , find BD and DC (ii) If AC=4.2cm , DC=6cm and BC=10cm , find AB . (iii) If AB=5.6cm , AC=6cm and DC=3cm , find BC .
View SolutionIn Figure, ABCD is a parallelogram. If AB=12cm,AE=7.5cm,CF=15cm, then AD=
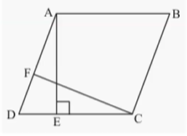
(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 10.5 cm
View SolutionIn Fig. 4.57, AE is the bisector of the exterior ∠CAD meeting BC produced in E . If AB=10cm , AC=6cm and BC=12cm , find CE . (FIGURE)
View SolutionIn right △ABC, the lengths of the legs are given. Find the length of the hypotenuse.
(i)a=6 cm, b=8 cm (ii) a=8 cm, b=15 cm (iii)a=3 cm, b=4 cm (iv) a=2 cm, b=1.5 cm
View SolutionIn a ABC , AD is the bisector of ∠BAC . If AB=6cm , AC=5cm and BD=3cm , then DC= 11.3cm (b) 2.5cm (c) 3:5cm (d) None of these
View Solution
