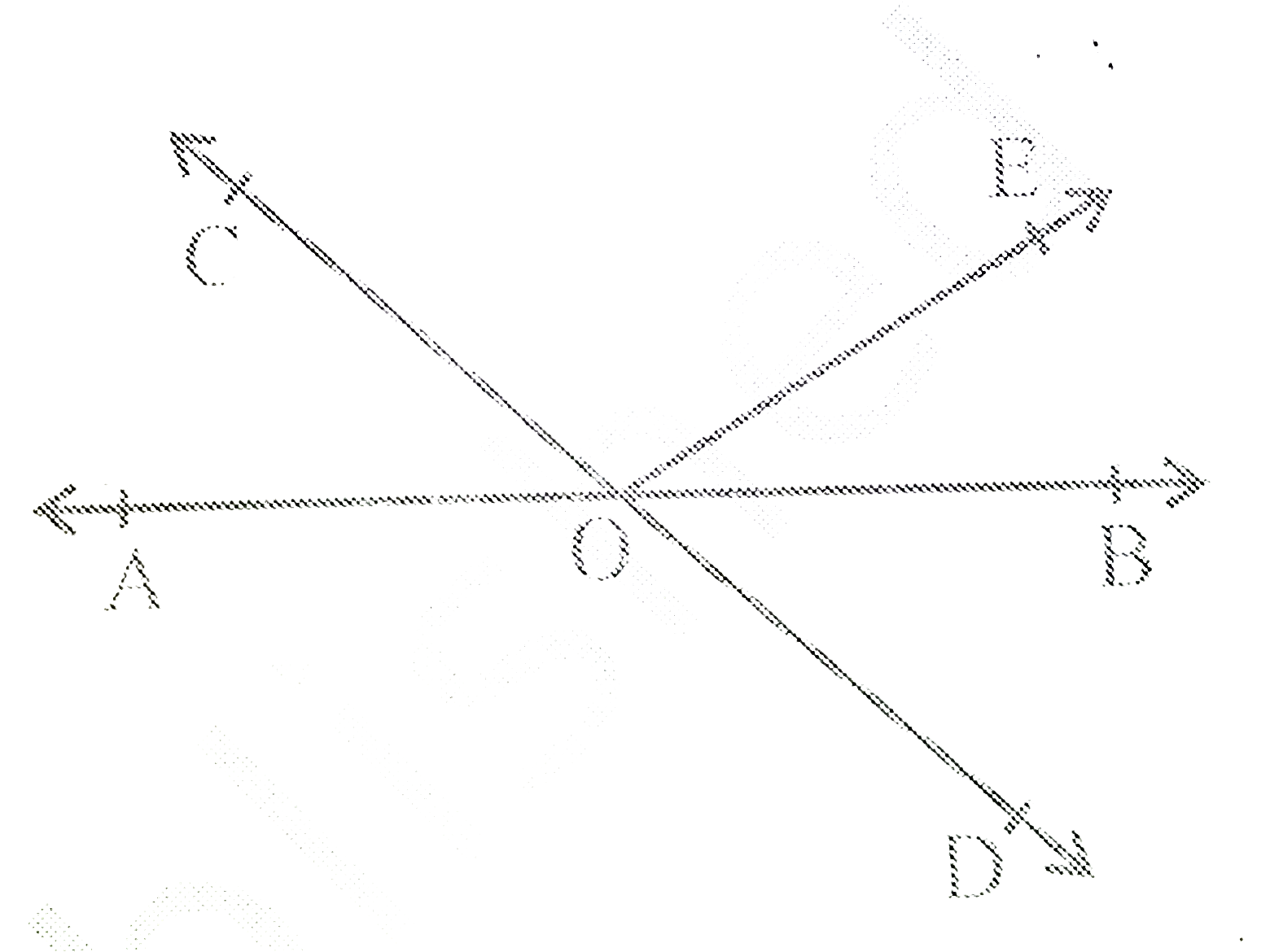Two lines AB and CD intersect at O. If ∠AOC+∠COB+∠BOD=2700 , find the measures of ∠AOC, ∠COB, ∠BOD and ∠DOA.
Solution
Let '/_AOC=x and /_COB=y'.
Then, '/_BOD=x' and /_DOA=y'
Now, '/_AOC+
/_COB+/_BOD=270 @'
⇒'x+y
+x=270@'
⇒'2x +y = 270@'
But, 'x+y=180@'
∴'x=y=90@'
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a quadrilateral ABCD, the bisectors of ∠A and ∠B meet at O. If ∠C=70∘and∠D=130∘, then measure of ∠AOBis
A40∘B60∘C80∘D100∘
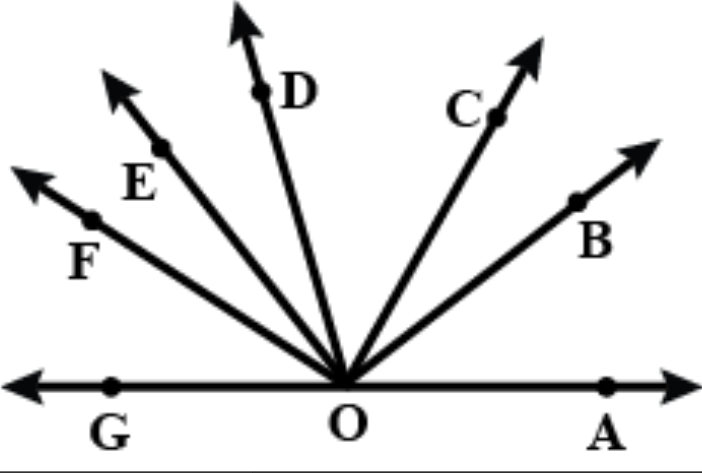
If Figure, ∠AOF and ∠FOG form a linear pair. ∠EOB= ∠FOC=9000and ∠DOC= ∠FOG= ∠AOB=300 Find the measure of ∠FOE, ∠COB and ∠DOE. Name all the right angles. Name three pairs of adjacent complementary angles. Name three pairs of adjacent supplementary angles. Name three pairs of adjacent angles.
 View Solution
View SolutionLine segments AB and CD intersect at O such that AC∣∣DB . If ∠CAB=350 and ∠CDB=550 find the ∠BOD.
View SolutionIn a parallelogram ABCD, if ∠D=115∘, then write the measure of ∠A
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8 cm and BD=5.6cm . Find the measures of OC and OD
View SolutionIn figure, ΔODCΔOBA,∠BOC=125oand ∠CDO=70o. Find∠DOC,∠DCOand∠OAB.
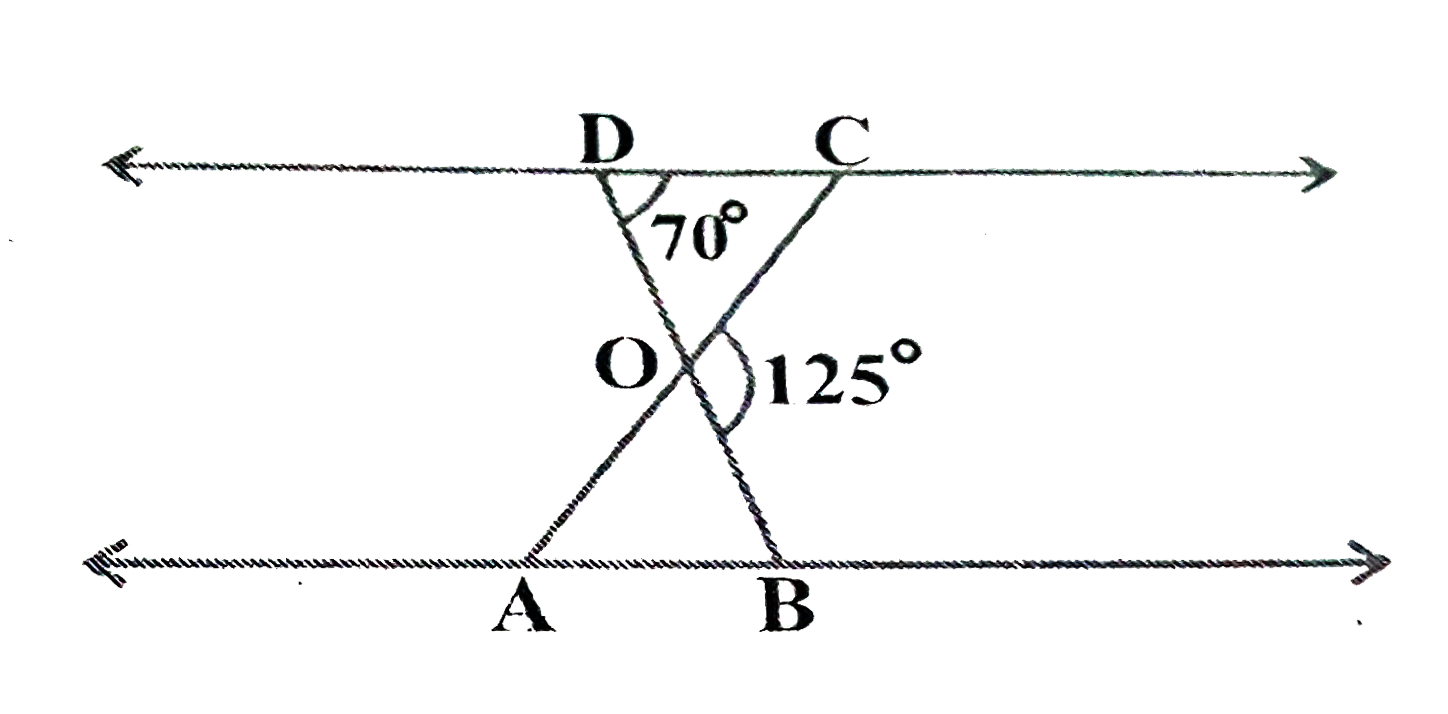 View Solution
View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
View Solution