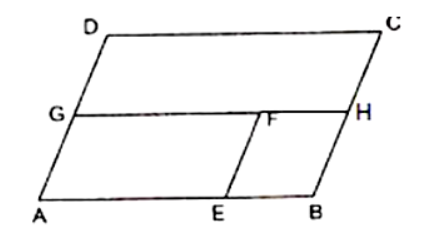
if ABDE and BDFG such that ∠FGH=1250 and ∠B=550, find x and y
We are given that : ∠FGH=125∘<br>and∠B=55∘<br>∠FGH+∠FGE=180∘(L∈earpair)<br>125+y=180∘<br>y=180−125=55∘<br>BA||FDandBD||FG<br>∠B=∠F=55∘<br>Now∈△EFG,<br>∠F+∠FEG+∠FGE=180∘
(Angles of a triangle)
= 55+x+55'180∘<br≥x+110∘=180∘<br>x=180−110∘=70∘<br>Hencex=70,y=55∘
Topper's Solved these Questions
Similar Questions
In Fig.84, ABCD and AECF; ∠FCG=900 and ∠BAC=1200. Find the values of x,y and z.
View SolutionIf ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View SolutionIn Fig.102, ABCDEF, ∠ABG=1100,∠GCD=1000 and ∠BGC=x0. the value of x is (a) 35 (b) 50 (c) 30 (d) 40
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn Figure, ABCD and AEFG are two parallelograms. If ∠C=580, find ∠F
 View Solution
View SolutionIn Fig.80, line ACl∈e DE and ∠ABD=320. Find out the angles x and y if ∠E=1220.
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(EBG)=ar(EFC)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that : ar(ADEG)=ar(GBCE) ar(EGB)=16ar(ABCD)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(ADEG)=ar(GBCE)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB ,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: Find what portion of the area of parallelogram is the area of EFG
View Solution

