If cos40∘=xandcosθ=1−2x2, then the possible values of θ lying between 0∘ and 360∘ is
100∘and260∘
80∘and280∘
280∘and110∘
110∘and260∘
The correct Answer is:A
To solve the problem, we start with the given equations:
1. cos40∘=x
2. cosθ=1−2x2
Step 1: Substitute x in the equation for cosθ
We know that x=cos40∘. Therefore, we can substitute x into the equation for cosθ:
cosθ=1−2(cos40∘)2
Step 2: Use the double angle identity
Using the double angle identity for cosine, we know that:
cos2A=2cos2A−1
Thus, we can rewrite 1−2(cos40∘)2 as:
cosθ=−cos80∘
Step 3: Set up the equation for θ
Now we have:
cosθ=−cos80∘
This implies:
cosθ=cos(180∘−80∘)orcosθ=cos(180∘+80∘)
Step 4: Solve for θ
From the above, we can find the possible values of θ:
1. θ=180∘−80∘=100∘
2. θ=180∘+80∘=260∘
Step 5: Conclusion
Thus, the possible values of θ lying between 0∘ and 360∘ are:
θ=100∘andθ=260∘
Final Answer:
The possible values of θ are 100∘ and 260∘.
---
2. cosθ=1−2x2
2. θ=180∘+80∘=260∘
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Competitive Thinking218videos
TRIGONOMETRIC FUNCTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Evaluation Test34videos
TRIGONOMETRIC FUNCTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Evaluation Test34videos
TRIGONOMETRIC FUNCTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - Evaluation Test9videos
THREE DIMENSIONAL GEOMETRY
- BOOK - TARGET PUBLICATIONCHAPTER - VECTORSEXERCISE - Evaluation Test18videos
VECTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
If K=cos20∘ and cosx=2K2−1, then the possible value of x between 0∘ and 360∘ are
A140∘B40∘,140∘C40∘,320∘D50∘,130∘ - Question 2 - Select One
The value of θ lying between 0 and π2 and satisfying the equation
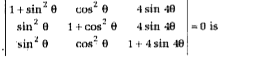 A7π24or11π24B5π24C3π24Dnone of these
A7π24or11π24B5π24C3π24Dnone of these - Question 3 - Select One
If sin32∘=kandcosx=1−2k2,α,β are the values of x between 0∘ and 360∘ with α<β, then
Aα+β=180∘Bβ−α=200∘Cβ=4α+40∘Dβ=5α−20∘
If cos θ=12(x+1x), what is the value of cos 2θ ?
View Solutionlf sin(x−y)−cos(x+y)=12 then the values of x&y lying between 0andπ are given by
View SolutionIf cosθ=−12and0∘<θ<360∘, then the values of θ are
View SolutionIf cosθ=−12 and 0<θ<360∘, then the value of θ are
View SolutionIf the eccentricity of the hyperbola x2(1+sinθ)2−y2cos2θ=1 is 2√3, then the sum of all the possible values of θ is (where, θ∈(0,π))
View Solution

