For the function z = 4x+ 9y to be maximum under the constraints x+5y≤200,2x+3y≤134,x≥0,y≥0 the values of x and y are
A
10,38
B
28,10
C
13,36
D
30,34
Video Solution
Text Solution
The correct Answer is:A
|
Answer
Step by step video, text & image solution for For the function z = 4x+ 9y to be maximum under the constraints x+5yle200,2x+3yle134,xge0,yge0 the values of x and y are by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Competitive Thinking35videos
LINEAR PROGRAMMING
- BOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Evaluation Test11videos
LINEAR PROGRAMMING
- BOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Evaluation Test11videos
LINEAR PROGRAMMING
- BOOK - TARGET PUBLICATIONCHAPTER - LINEEXERCISE - Evaluation Test1videos
LINE
- BOOK - TARGET PUBLICATIONCHAPTER - MATHEMATICAL LOGIC EXERCISE - EVALUATION TEST14videos
MATHEMATICAL LOGIC
Similar Questions
Knowledge Check
- Question 1 - Select One
The constraints −x+y≤1,−x+3y≤9,x≥0,y≥0 defines
Abounded feasible regionBunbounded feasible regionCboth bounded and unbounded regionDunique solution - Question 2 - Select One
Shaded, region of the constraints 4x+3y≤12,−x+y≤2,x≥0,y≥0 is
A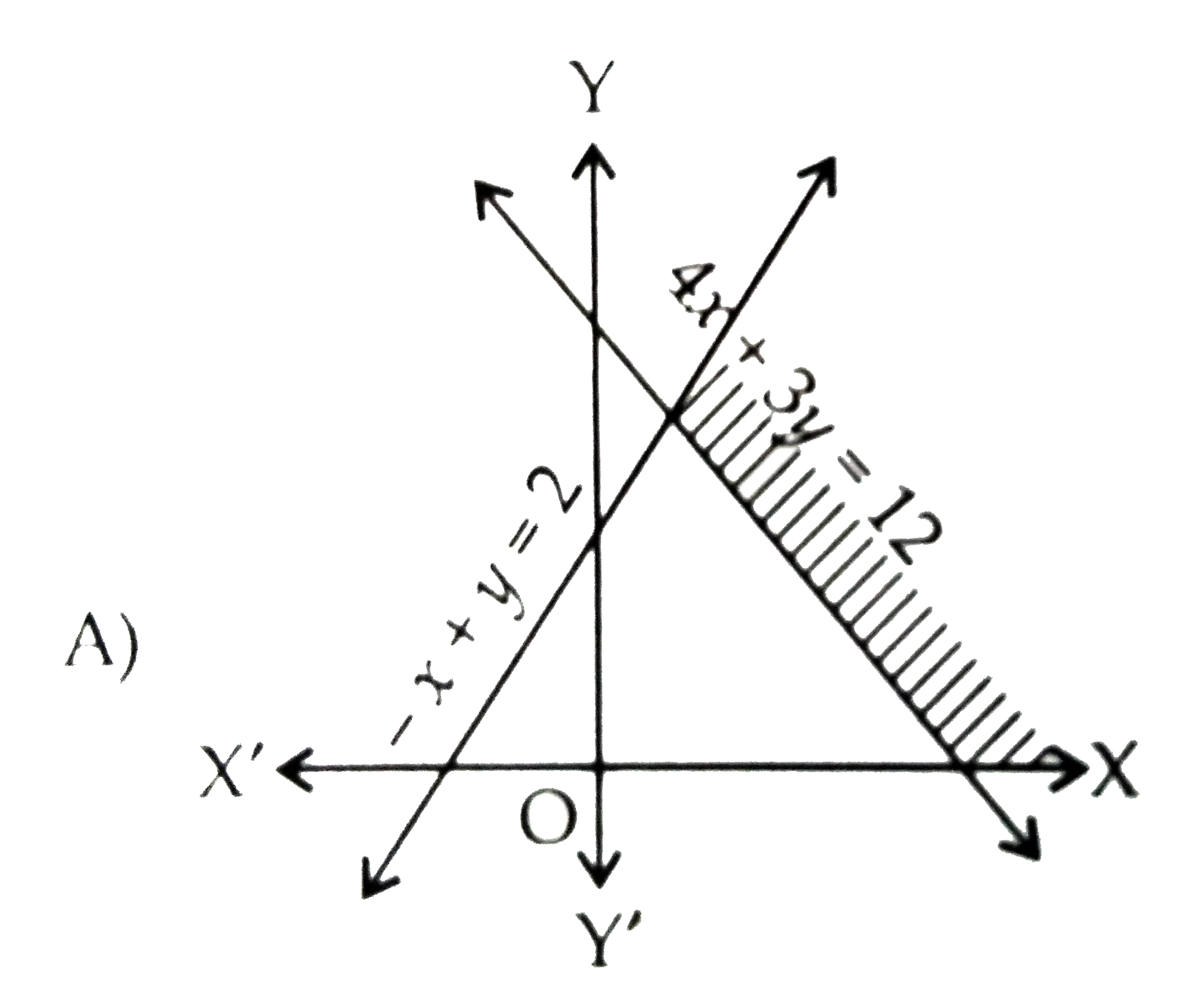 B
B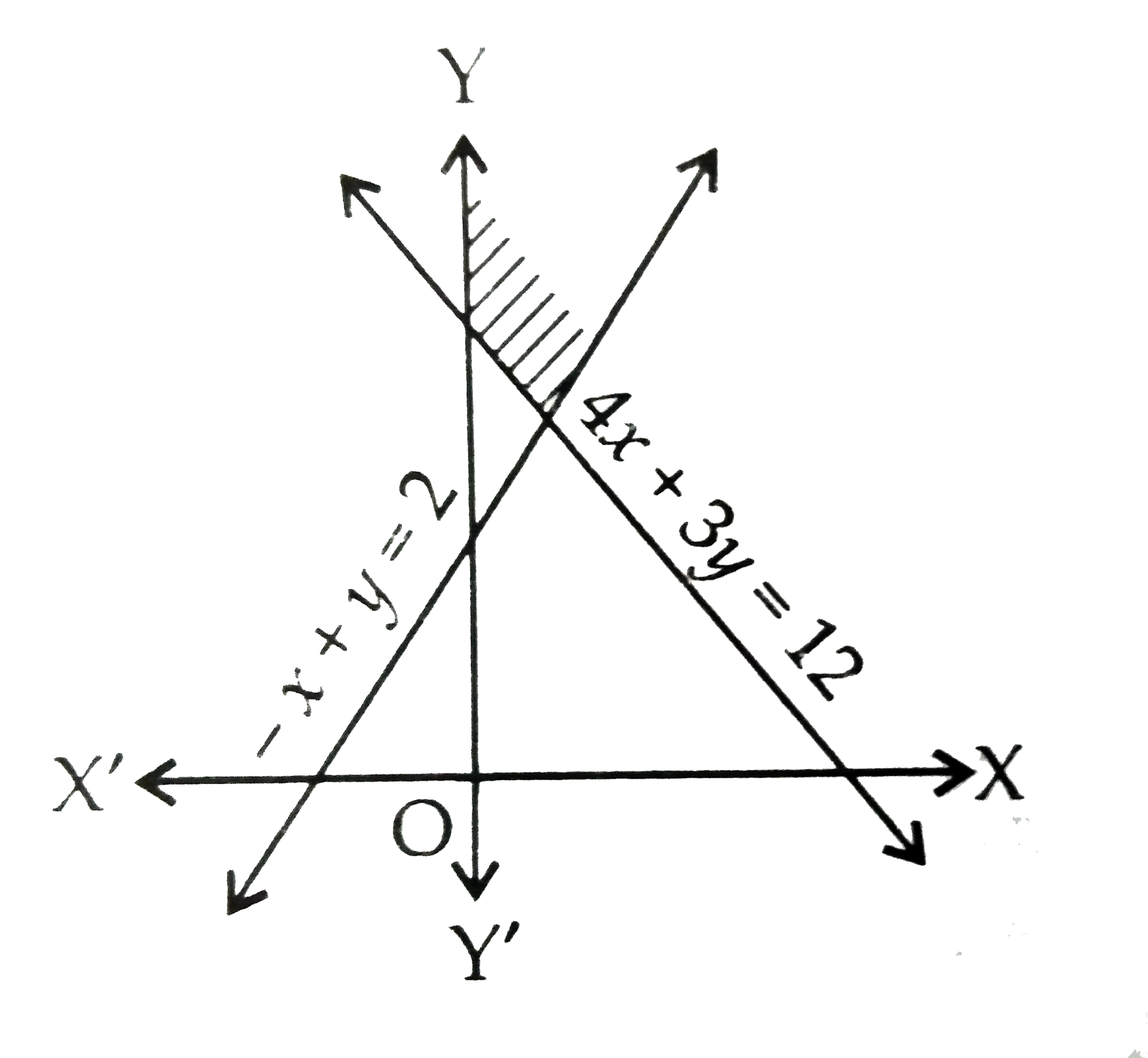 C
C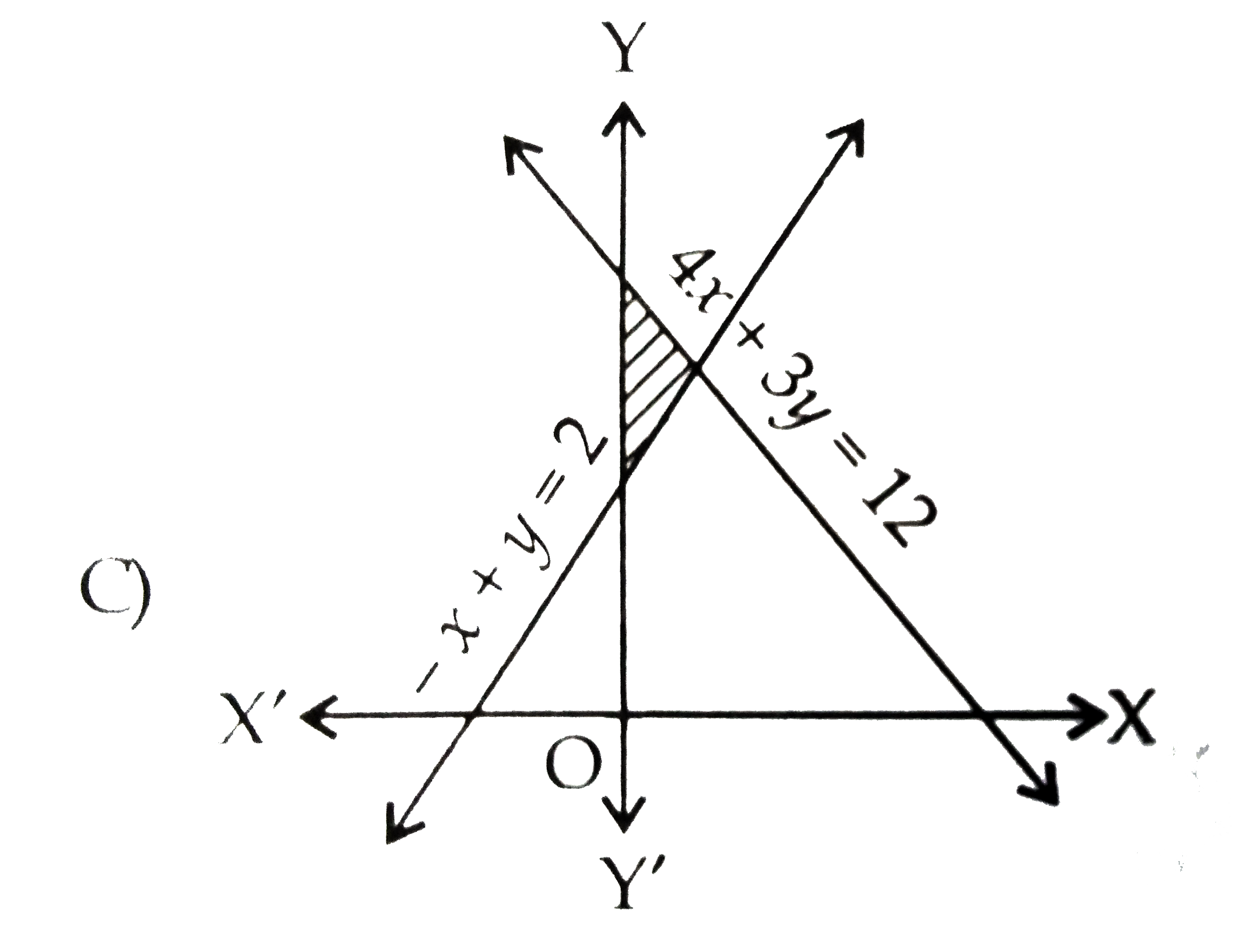 D
D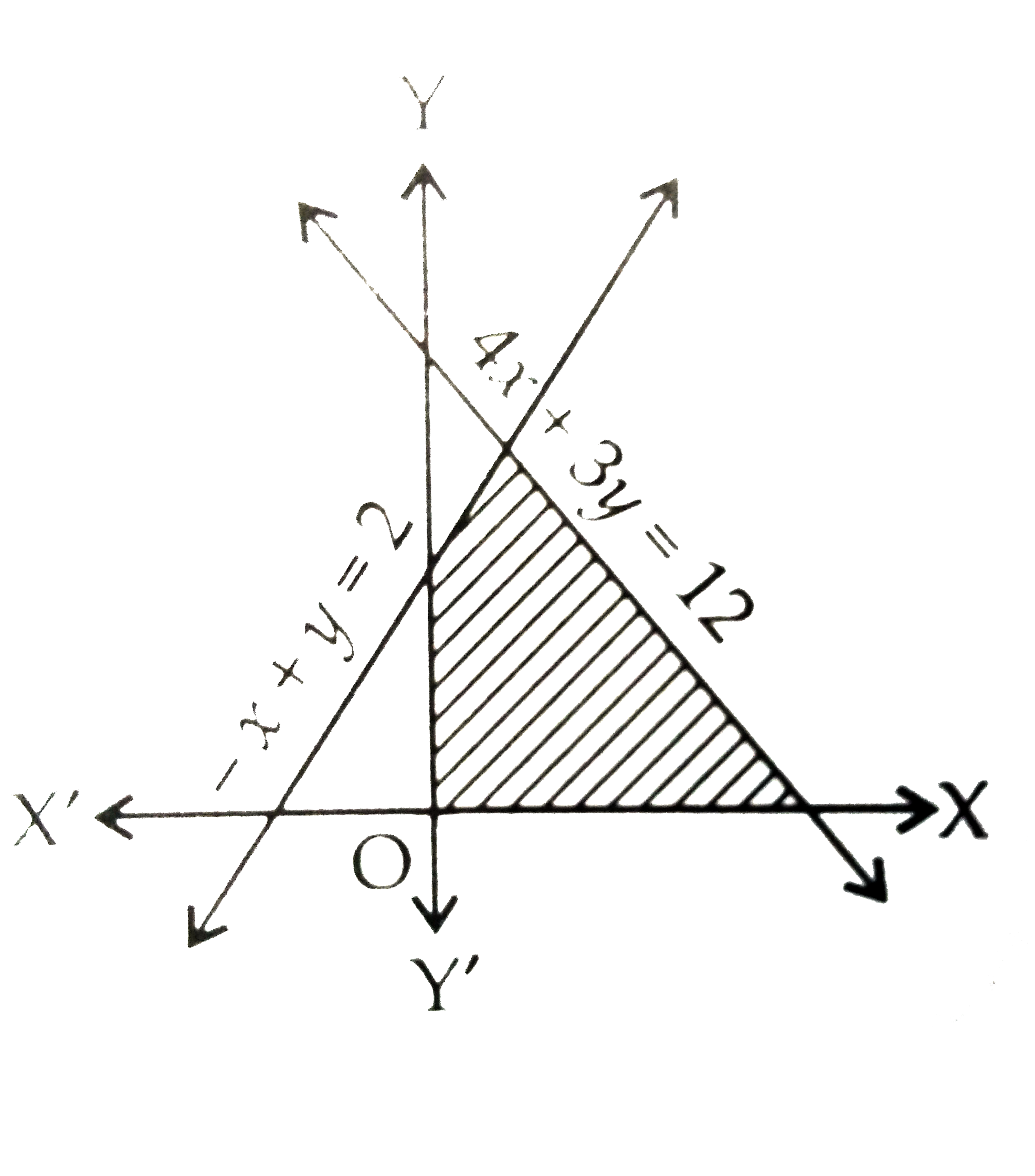
- Question 3 - Select One
The constraints x+y≤8,2x+3y≤12,x≥0,y≥0 and the objective function z=4x+6y has
Aconcave solutionBno unique solutionCbounded solutionDunique solution
The contraints −x+y≤1,−x+3y≤9,x≥0,y≥0 of LLP correspond to
View SolutionThe constraints x−y≥0,−x+3y≤3,x≥0,y≥0 and the objective function z=6x+8y has
View SolutionShaded, region of the constraints x+y≥5,2x+3y≤18,4x+3y≤24,x≥0,y≥0 is
View SolutionThe constraints 3x+2y≥9,x−y≤3,x≥0,y≥0 and the objective function z=4x+2y has
View SolutionThe constraints x+2y≤2,2x+4y≥8,x≥0,y≥0 and the objective function z=7x−3y has
View Solution

