There are four point masses m each on the corners of a square of side length I about one of its diagonals, the moment of inertia of the system is
2ml2
ml2
4ml2
6ml2
The correct Answer is:B
To find the moment of inertia of the system of four point masses located at the corners of a square of side length L about one of its diagonals, we can follow these steps:
Step 1: Understand the Configuration
We have a square with four point masses m at each corner. The square has a side length L. We need to calculate the moment of inertia about one of its diagonals.
Step 2: Identify the Diagonal
The diagonal of the square divides it into two equal triangles. The length of the diagonal d can be calculated using the Pythagorean theorem:
d=√L2+L2=L√2
Step 3: Determine the Distance from the Diagonal
For the calculation of the moment of inertia, we need to find the perpendicular distance of each mass from the diagonal. The distance from the center of the square to the diagonal is L√2.
Step 4: Calculate the Moment of Inertia for Each Mass
The moment of inertia I for a point mass is given by:
I=mr2
where r is the distance from the axis of rotation. For the two masses that are perpendicular to the diagonal, the distance r is L√2.
Thus, the moment of inertia for one mass is:
I1=m(L√2)2=mL22
Step 5: Total Moment of Inertia
Since there are two masses contributing to the moment of inertia about the diagonal, the total moment of inertia Itotal is:
Itotal=2×I1=2×mL22=mL2
Step 6: Conclusion
The moment of inertia of the system about one of its diagonals is:
I=mL2
We have a square with four point masses m at each corner. The square has a side length L. We need to calculate the moment of inertia about one of its diagonals.
The diagonal of the square divides it into two equal triangles. The length of the diagonal d can be calculated using the Pythagorean theorem:
d=√L2+L2=L√2
For the calculation of the moment of inertia, we need to find the perpendicular distance of each mass from the diagonal. The distance from the center of the square to the diagonal is L√2.
The moment of inertia I for a point mass is given by:
I=mr2
where r is the distance from the axis of rotation. For the two masses that are perpendicular to the diagonal, the distance r is L√2.
I1=m(L√2)2=mL22
Since there are two masses contributing to the moment of inertia about the diagonal, the total moment of inertia Itotal is:
Itotal=2×I1=2×mL22=mL2
The moment of inertia of the system about one of its diagonals is:
I=mL2
Similar Questions
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be:
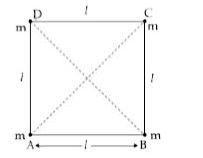 View Solution
View SolutionFour spheres of diameter a and mass m each are arranged at the corners of a square of side 1. Calculate the moment of inertia of the system about CD taken as its axis.
View Solution
Knowledge Check
- Question 1 - Select One
Four particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis perpendicular to the plane of frame and passing through a corner is
AML2B2ML2C2√2ML2D4ML2 - Question 2 - Select One
Four particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis passing through opposite corners of frame is
A√2ML2B2ML2CML2D2√2ML2 - Question 3 - Select One
Four particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis passing through any side of frame is
A4ML2B2√2ML2C2ML2D√2ML2
Four point masses of 20 g each are placed at the corners of a square ABCD of side 5 cm, as shown in Fig. 8.48. find the moment of inertia of the system (i) about an axis coinciding with the side BC and (ii) about an axis through A and perpendicular to the plane of the square.
 View Solution
View SolutionFour point masses of 5 g each are placed at the four corners fo a square of side 10 cm. Find the moment of inertia of the system (i) about an axis coinciding with one of the sides and (ii) about an axis passing through the point of intersection of the diagonals and perpendicular to the plane of the square.
View SolutionThree point masses each of mass m are placed at the corners of an equilateral triangle of side 'a' . Then the moment of inertia of this system about an axis passing along one side of the triangle is
View SolutionThree point masses each of mass m are placed at the corners of an equilateral triangle of side 'a'. Then the moment of inertia of this system about an axis passing along one side of the triangle is
View SolutionFour point masses each of value m, are placed at the corners of a square ABCD of side l, The moment of inertia of the system about an axis passing throught A and parallel to BD is
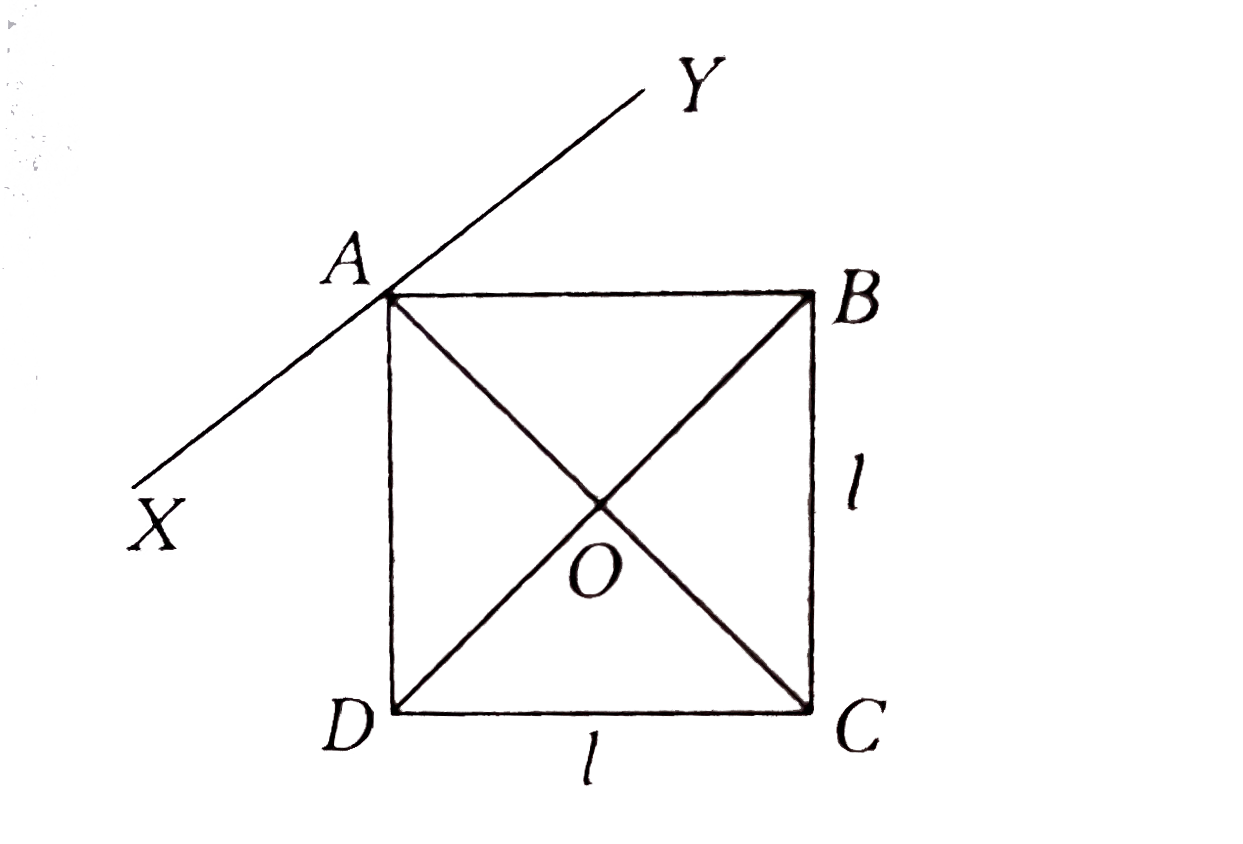 View Solution
View Solution

