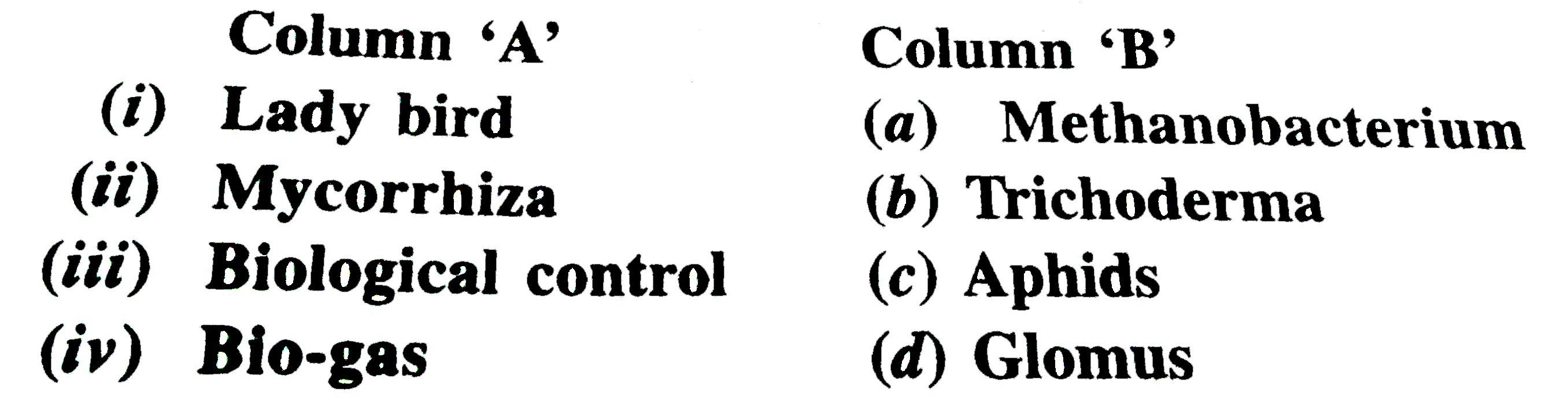Choose the correct answer
Every identity matrix is scalar matrix
Every scalar matrix is and identity matrix
Every diagonal matrix is an identity matrix
A square matrix whose each element is 1 is an identity matrix
The correct Answer is:A
To solve the question, we need to analyze each statement regarding matrices and determine their validity. Let's break down the statements one by one.
1. Understanding Identity Matrix:
- An identity matrix is a square matrix where all the diagonal elements are 1, and all non-diagonal elements are 0. For example, a 3x3 identity matrix looks like this:
I=⎛⎜⎝100010001⎞⎟⎠
Hint: Recall that the identity matrix acts as the multiplicative identity in matrix multiplication.
2. Understanding Scalar Matrix:
- A scalar matrix is a square matrix where all the diagonal elements are equal (let's say k), and all non-diagonal elements are 0. For example, a 3x3 scalar matrix could look like this:
S=⎛⎜⎝k000k000k⎞⎟⎠
Hint: Remember that a scalar matrix is a special case of a diagonal matrix where all diagonal elements are equal.
3. Understanding Diagonal Matrix:
- A diagonal matrix is a matrix where all non-diagonal elements are 0, but the diagonal elements can be any values (not necessarily equal). For example:
D=⎛⎜⎝a000b000c⎞⎟⎠
Hint: Diagonal matrices can have different values on the diagonal.
4. Analyzing Each Statement:
- Statement A: "Every identity matrix is a scalar matrix."
- This is True because an identity matrix has all diagonal elements equal to 1, which satisfies the definition of a scalar matrix.
- Statement B: "Every scalar matrix is an identity matrix."
- This is False because a scalar matrix can have diagonal elements equal to any constant k, not just 1.
- Statement C: "Every diagonal matrix is an identity matrix."
- This is False because diagonal matrices can have different values on the diagonal.
- Statement D: "A square matrix whose each element is one is an identity matrix."
- This is False because a matrix with all elements equal to 1 does not have 0s in the non-diagonal positions, thus it is not an identity matrix.
5. Conclusion:
- The only true statement is Statement A: "Every identity matrix is a scalar matrix."
Final Answer:
The correct answer is Statement A.
- An identity matrix is a square matrix where all the diagonal elements are 1, and all non-diagonal elements are 0. For example, a 3x3 identity matrix looks like this:
I=⎛⎜⎝100010001⎞⎟⎠
- A scalar matrix is a square matrix where all the diagonal elements are equal (let's say k), and all non-diagonal elements are 0. For example, a 3x3 scalar matrix could look like this:
S=⎛⎜⎝k000k000k⎞⎟⎠
- A diagonal matrix is a matrix where all non-diagonal elements are 0, but the diagonal elements can be any values (not necessarily equal). For example:
D=⎛⎜⎝a000b000c⎞⎟⎠
- Statement A: "Every identity matrix is a scalar matrix."
- This is True because an identity matrix has all diagonal elements equal to 1, which satisfies the definition of a scalar matrix.
- This is False because a scalar matrix can have diagonal elements equal to any constant k, not just 1.
- This is False because diagonal matrices can have different values on the diagonal.
- This is False because a matrix with all elements equal to 1 does not have 0s in the non-diagonal positions, thus it is not an identity matrix.
- The only true statement is Statement A: "Every identity matrix is a scalar matrix."
The correct answer is Statement A.