If the frequency of revolution of electron in an orbit H atom is n then the equivalent current is
en
The correct Answer is:D
To find the equivalent current when the frequency of revolution of an electron in an orbit of a hydrogen atom is n, we can follow these steps:
1. Understand the Concept of Current:
Current (I) is defined as the charge (Q) that flows per unit time (t). Mathematically, it can be expressed as:
I=Qt
2. Identify the Charge of the Electron:
The charge of an electron (e) is approximately 1.6×10−19 coulombs.
3. Relate Frequency to Time:
The frequency (n) of revolution indicates how many times the electron completes a full orbit in one second. Therefore, the time period (T) for one complete revolution is the reciprocal of frequency:
T=1n
4. Calculate the Current:
Since the electron completes n revolutions in one second, the total charge that passes through a point in one second is the charge of the electron multiplied by the frequency:
I=Q×n=e×n
5. Substitute the Charge of the Electron:
Now, substituting the value of Q (which is e):
I=e⋅n
6. Conclusion:
Thus, the equivalent current when the frequency of revolution of the electron in the orbit of a hydrogen atom is n is:
I=e⋅n
Final Answer:
The equivalent current is e⋅n.
Current (I) is defined as the charge (Q) that flows per unit time (t). Mathematically, it can be expressed as:
I=Qt
The charge of an electron (e) is approximately 1.6×10−19 coulombs.
The frequency (n) of revolution indicates how many times the electron completes a full orbit in one second. Therefore, the time period (T) for one complete revolution is the reciprocal of frequency:
T=1n
Since the electron completes n revolutions in one second, the total charge that passes through a point in one second is the charge of the electron multiplied by the frequency:
I=Q×n=e×n
Now, substituting the value of Q (which is e):
I=e⋅n
Thus, the equivalent current when the frequency of revolution of the electron in the orbit of a hydrogen atom is n is:
I=e⋅n
The equivalent current is e⋅n.
Topper's Solved these Questions
Similar Questions
(a) Find the frequencies of revolution of electrons in n = 1 and n=2 Bohr orbits.
(b)What is the frequency of the photon emitted when an electron in an n=2 orbit drops to an n=1 hydrogen orbit?
(c )An electron typically spends about 10−8s∈anexcitedstatebeforeitdrops→alowerstatebyemie∈gapho→n.Howmanyrevolutionsdoesane≤ctron∈ann=2Bohrhydro≥norbitmake∈100xx10^(-8) s?.View SolutionA: In Bohr model , the frequency of revolution of an electron in its orbit is not connected to the frequency of spectral line for smaller principal quantum number n.
R: For transitions between large quantum number the frequency of revolution of an electron in its orbit is connected to the frequency of spectral line, as per Bohr's Correspondence principle.View Solution
Knowledge Check
- Question 1 - Select One
Energy of electron in a orbit of H -atom is
APositiveBNegativeCZeroDNothing can be said - Question 2 - Select One
Find the frequency of revolution of the electron in the first orbit of H-atom
A6×1014HzB6.6×1010HzC6.6×10−10HzD6.6×1015Hz - Question 3 - Select One
If in hydrogen atom, radius of nth Bohr orbit is rn., frequency of revolution of electron in nth orbit is fn choose the correct option.
A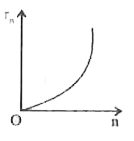
B
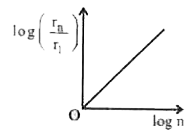C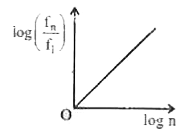
DBoth (a) and (b)
If in hydrogen atom, radius of nth Bohr orbit is , nr frequency of revolution of electron in nth orbit is fn choose the correct option
View SolutionFrequency of revolution of electron in the nth Bohr's orbit is given by
View SolutionThe frequency of revolution of an electron in nth orbit is fn. If the electron makes a transition from nth orbit to (n=1) th orbit , then the relation between the frequency (v) of emitted photon and fn will be
View SolutionIn an atom, an electron moves in an orbit of radius r with a speed v, the equivalent current is.
View SolutionIf, in a hydrogen atom, radius of nth Bohr orbit is rn frequency of revolution of electron in nth orbit is fn and area enclosed by the nth orbit is An , then which of the pollowing graphs are correct?
View Solution