If f(0)=0=g(0)andf'(0)=6=g'(0)thenlimx→0f(x)g(x)=
A
−1
B
0
C
1
D
12
Video Solution
Text Solution
The correct Answer is:C
|
Answer
Step by step video, text & image solution for If f(0)=0=g(0)and f'(0)=6=g'(0)then lim_(xrarr0)f(x)/g(x)= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - I : CHAPTER 11)19videos
DIFFERENTIATION
- BOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - II : CHAPTER 11)24videos
DIFFERENTIATION
- BOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - TEST YOUR GRASP14videos
DIFFERENTIAL EQUATIONS
- BOOK - MARVEL PUBLICATIONCHAPTER - INTEGRATION - DEFINITE INTEGRALS EXERCISE - TEST YOUR GRASP20videos
INTEGRATION - DEFINITE INTEGRALS
Similar Questions
Knowledge Check
- Question 1 - Select One
Let fandg be real valued functions defined on interval (−1,1) such that g''(x) is constinous, g(0)=0, g'(0)=0,g''(0)=0andf(x)=g(x)sinx.
Statement I limx→0(g(x)cotx−g(0)cosecx)=f''(0)
Statement II f'(0)=g'(0)ABoth statement I and Statement II are correct and Statement II is the correct explanation of Statement IBBoth Statement I and Statement II are correct but Statement II is not the correct explanation of Statement ICStatement I is correct but Statement II is incorrectDStatement II is correct but Statement I is incorrect. - Question 2 - Select One
Let f:R→Rbe differentiable at x = 0. If f(0) = 0 and f'(0)=2, then the value of
limx→01x[f(x)+f(2x)+f(3x)+….+f(2015x)] isA2015B0C2015×2016D2015×2014 - Question 3 - Select One
If g(x)=(x2+2x+3)f(x),f(0)=5 and limx→0(f(x)−5x)=4, then g'(0) is equal to
A22B18C20D25
If f(x)={x,x≤0and−x,x>0andg(x)=f(x)+|x| then limx→0+(log|sinx|x)g(x)=
View SolutionLet f(x+y)=f(x)f(y)andf(x)=1+xg(x)G(x) where limx→0g(x)=aandlimx→oG(x)=b.Then f'(x) is
View SolutionEvaluate limx→0f(x), where
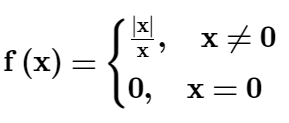 View Solution
View SolutionIf g(x)=(x2+3x+1)f(x),f(0)=3andlimx→0f(x)−3x=2, then g'(0)= (i)3 (ii)12 (iii)6 (iv)11
View SolutionIf limx→0[1+x+f(x)x]1/x=e3, then limx→0[1+f(x)x]1/x=
View Solution

