An aqueous solution of urea is found to boil at 100.52∘C. Given Kb for water is 0.52 K kg mol−1, the mole fraction of urea in the solution is
1
0.5
0.018
0.25
The correct Answer is:C
To solve the problem of finding the mole fraction of urea in an aqueous solution that boils at 100.52°C, we can follow these steps:
Step 1: Calculate the boiling point elevation (ΔTb)
The boiling point elevation is given by the formula:
ΔTb=Tb(solution)−Tb(solvent)
Where:
- Tb(solution)=100.52°C
- Tb(solvent)=100°C (boiling point of pure water)
Calculating ΔTb:
ΔTb=100.52°C−100°C=0.52°C
Step 2: Use the boiling point elevation formula to find molality (m)
The relationship between boiling point elevation and molality is given by:
ΔTb=Kb⋅m
Where:
- Kb=0.52K kg mol−1
Rearranging the formula to find molality:
m=ΔTbKb
Substituting the values:
m=0.520.52=1mol/kg
Step 3: Determine the number of moles of urea
Since the molality is defined as the number of moles of solute per kilogram of solvent, we have:
- 1 mole of urea in 1 kg of water.
Step 4: Calculate the number of moles of water
To find the mole fraction, we need the number of moles of water. The molecular weight of water (H2O) is approximately 18 g/mol.
Given that we have 1 kg (or 1000 g) of water:
Number of moles of water=massmolar mass=1000g18g/mol≈55.55mol
Step 5: Calculate the mole fraction of urea
The mole fraction (X) of urea is given by:
Xurea=moles of ureamoles of urea+moles of water
Substituting the values:
Xurea=11+55.55=156.55≈0.0177
Final Answer
Thus, the mole fraction of urea in the solution is approximately:
Xurea≈0.018
The boiling point elevation is given by the formula:
ΔTb=Tb(solution)−Tb(solvent)
Where:
- Tb(solution)=100.52°C
- Tb(solvent)=100°C (boiling point of pure water)
ΔTb=100.52°C−100°C=0.52°C
The relationship between boiling point elevation and molality is given by:
ΔTb=Kb⋅m
Where:
- Kb=0.52K kg mol−1
m=ΔTbKb
m=0.520.52=1mol/kg
Since the molality is defined as the number of moles of solute per kilogram of solvent, we have:
- 1 mole of urea in 1 kg of water.
To find the mole fraction, we need the number of moles of water. The molecular weight of water (H2O) is approximately 18 g/mol.
Number of moles of water=massmolar mass=1000g18g/mol≈55.55mol
The mole fraction (X) of urea is given by:
Xurea=moles of ureamoles of urea+moles of water
Xurea=11+55.55=156.55≈0.0177
Thus, the mole fraction of urea in the solution is approximately:
Xurea≈0.018
Topper's Solved these Questions
- SOLUTIONSBOOK - PRADEEPCHAPTER - SOLUTIONSEXERCISE - Competition (FOCUS) JEE (Main and Advanced)/Medical Entrance SPECIAL (II. Multiple Choice Question )
7 Videos
- SOLUTIONSBOOK - PRADEEPCHAPTER - SOLUTIONSEXERCISE - Competition (FOCUS) JEE (Main and Advanced)/Medical Entrance SPECIAL (III. Multiple Choice Question )
13 Videos
- SOLUTIONSBOOK - PRADEEPCHAPTER - SOLUTIONSEXERCISE - VALUE BASED QUESTIONS WITH ANSWERS
7 Videos
- REDOX REACTIONS BOOK - PRADEEPCHAPTER - REDOX REACTIONS EXERCISE - Assertion reason type question
16 Videos
- SOME BASIC CONCEPTS OF CHEMISTRYBOOK - PRADEEPCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - Competition (FOCUS) JEE (Main and Advanced)/Medical Entrance SPECIAL (VIII. Assertion-Reason Type Questions)(Type II)
13 Videos
Similar Questions
Knowledge Check
Elevation in boiling point of an aqueous solution of urea is 0.52(kbfor water=0.52Kmolality−1). The mole fraction is urea in this solution is :
A0.98B0.0567C0.943D0.02Consider following figure and answer the questions at the end of it.
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
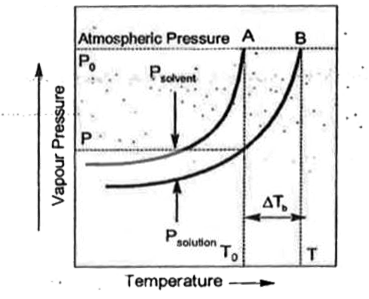
Variation of vapour pressure with temperature and showing elevation in boiling point.
Elevation in boiling point of an aqueous urea solution is 0.52∘. (Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution isA0.982B0.0567C0.943D0.018Pure water boils at 99.725∘C at Shimla. If Kb for water is 0.51Kmol−1kg the boiling point of 0.69 molal urea solution will be:
A100.079∘CB103∘CC100.359∘CDun predictable
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Elevation in b.p of an aqueous urea solution is 0.52∘(Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution is:
View SolutionConsider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
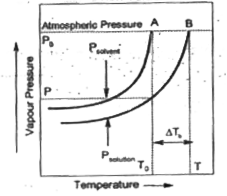
Variation of vapour pressure with temperature and showing elevation in boiling point.
Elevation in boiling point of an aqueous urea solution is 0.52∘.(Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution is:
View SolutionAt certain Hill-station pure water boils at 99.725∘C. If Kb for water is 0.513∘Ckgmol−1, the boiling point of 0.69m solution of urea will be:
View SolutionAn aqueous solution freezes on 0.36∘CKfandKb for water are 1.8 and 0.52 k kg mol−1 respectively then value of boiling point of solution as 1 atm pressure is
View SolutionDepression in f.p. of an aqueous urea solutio is 1.86∘.(Kf=1.86∘mol−1kg) Hence, mole− fraction of urea in this soluiton is :
View Solution
