The following rate data were obtained for the thermal decomposition of N2O5(g)
2N2O5(g)→2N2O4(g)+O2(g)
Time (sec)050Total pressure (atm)0.20.25
Calculate the reaction rate when the total pressure is 0.28 atm
The correct Answer is:Rate =5.54×10−4 atm s−1
To solve the problem of calculating the reaction rate for the thermal decomposition of N2O5(g) when the total pressure is 0.28 atm, we can follow these steps:
Step 1: Understand the Reaction
The reaction is given as:
2N2O5(g)→2N2O4(g)+O2(g)
Step 2: Analyze Initial and Final Conditions
From the data provided:
- At t=0 seconds, the total pressure Ptotal=0.20 atm.
- At t=50 seconds, the total pressure Ptotal=0.25 atm.
Step 3: Calculate the Change in Pressure
The change in pressure over the 50 seconds can be calculated as:
- Initial pressure of N2O5 at t=0: PN2O5=0.20 atm.
- At t=50 seconds, the total pressure is 0.25 atm.
The increase in pressure is due to the formation of products. The relationship can be expressed as:
Ptotal=PN2O5+PN2O4+PO2
Step 4: Determine the Pressure at t=50 seconds
From the stoichiometry of the reaction:
- For every 2 moles of N2O5 that decompose, 2 moles of N2O4 and 1 mole of O2 are produced.
- Let P be the pressure of N2O5 that decomposed.
At t=50 seconds:
Ptotal=0.20+P2
Setting this equal to 0.25 atm gives:
0.20+P2=0.25
P2=0.05
P=0.10 atm
Step 5: Calculate the Pressure of N2O5 at t=50 seconds
The remaining pressure of N2O5 is:
PN2O5=0.20−P=0.20−0.10=0.10 atm
Step 6: Calculate the Rate Constant K
Using the first-order rate equation:
K=2.303tlog(AA−x)
Where:
- A=0.20 atm (initial pressure of N2O5)
- x=P=0.10 atm (pressure of N2O5 decomposed)
Substituting into the equation:
K=2.30350log(0.200.10)
K=2.30350log(2)
Calculating gives:
K≈0.01386 s−1
Step 7: Calculate the Rate at Ptotal=0.28 atm
Now, when Ptotal=0.28 atm:
0.28=0.20+P2
Solving for P:
P2=0.08
P=0.16 atm
Step 8: Calculate the Remaining Pressure of N2O5
The pressure of N2O5 at this point:
PN2O5=0.20−P=0.20−0.16=0.04 atm
Step 9: Calculate the Reaction Rate
The rate of the reaction is given by:
Rate=K×PN2O5
Substituting the values:
Rate=0.01386×0.04
Calculating gives:
Rate≈5.54×10−4 atm/s
Final Answer
The reaction rate when the total pressure is 0.28 atm is approximately 5.54×10−4 atm/s.
---
The reaction is given as:
2N2O5(g)→2N2O4(g)+O2(g)
From the data provided:
- At t=0 seconds, the total pressure Ptotal=0.20 atm.
- At t=50 seconds, the total pressure Ptotal=0.25 atm.
The change in pressure over the 50 seconds can be calculated as:
- Initial pressure of N2O5 at t=0: PN2O5=0.20 atm.
- At t=50 seconds, the total pressure is 0.25 atm.
Ptotal=PN2O5+PN2O4+PO2
From the stoichiometry of the reaction:
- For every 2 moles of N2O5 that decompose, 2 moles of N2O4 and 1 mole of O2 are produced.
- Let P be the pressure of N2O5 that decomposed.
Ptotal=0.20+P2
Setting this equal to 0.25 atm gives:
0.20+P2=0.25
P2=0.05
P=0.10 atm
The remaining pressure of N2O5 is:
PN2O5=0.20−P=0.20−0.10=0.10 atm
Using the first-order rate equation:
K=2.303tlog(AA−x)
Where:
- A=0.20 atm (initial pressure of N2O5)
- x=P=0.10 atm (pressure of N2O5 decomposed)
K=2.30350log(0.200.10)
K=2.30350log(2)
Calculating gives:
K≈0.01386 s−1
Now, when Ptotal=0.28 atm:
0.28=0.20+P2
Solving for P:
P2=0.08
P=0.16 atm
The pressure of N2O5 at this point:
PN2O5=0.20−P=0.20−0.16=0.04 atm
The rate of the reaction is given by:
Rate=K×PN2O5
Substituting the values:
Rate=0.01386×0.04
Calculating gives:
Rate≈5.54×10−4 atm/s
The reaction rate when the total pressure is 0.28 atm is approximately 5.54×10−4 atm/s.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - CHEMICAL KINETICSEXERCISE - CURIOSITY QUESTION2videos
CHEMICAL KINETICS
- BOOK - PRADEEPCHAPTER - CHEMICAL KINETICSEXERCISE - TEST YOUR GRIP (MULTIPLE CHOICE QUESTIONS)25videos
CHEMICAL KINETICS
- BOOK - PRADEEPCHAPTER - CHEMICAL KINETICSEXERCISE - ADVANCED PROBLEMS FOR COMPETITIONS14videos
CHEMICAL KINETICS
- BOOK - PRADEEPCHAPTER - BIOMOLECULES EXERCISE - IMPORTANT QUESTIONS (FOR BOARD EXAMINATION)25videos
BIOMOLECULES
- BOOK - PRADEEPCHAPTER - CHEMISTRY IN EVERYDAY LIFE EXERCISE - IMPORTANT QUESTION FOR BOARD EXAMINATION30videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
The following data were obtained during the first order thermal decomposition of N2O5 (g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
(S.no,Time,Total Pressure / atm),(1,0,0,5),(2,100,0.512)
Calculate the rate constant.View SolutionThe following data were obtained during the first thermal decompoistion of N2O5(g) at constant volume.
2N2O5(g)→2N2O4(g)+O2(g)
∣∣ ∣ ∣∣S.No.Time (s)Total pressure (atm)i.00.5ii.1000.512∣∣ ∣ ∣∣
Calculate the rate constant.View Solution
Knowledge Check
- Question 1 - Select One or More
For the first order reaction
2N2O5(g)→4NO2(g)+O2(g)Athe concentration of the reactant decreases exponentially with time .Bthe half -life of the reaction decreases with increasing temperature .Cthe half - life of the reaction depends on the initial concentration of the reachantDthe reaction proceed to 99.6 % completon eight half - life duration . - Question 2 - Select One
For the first order reaction
2N2O5(g)→4NO2(g)+O2(g)AThe concentration of the reaction decreases exponentially with timeBThe half-life of the reaction decreases with increasing temperatureCThe half-life of the reaction depends on the initial concentration of the reactantDThe reaction proceeds to 99.6 % completion in eight half-life duration - Question 3 - Select One or More
For the first order reaction
2N2O5(g)→4NO2(g)+O2(g)AThe concentration of the reactant decreases exponentially with time.BThe half life of the reaction decreases with increaisng temperature.CThe half life of the reaction depends on the initial concentration of the reactant.DThe reaction proceeds to 99.6% completion in 8 half. Life durations.
The following data were obtained the first order thermal decomposition of N2O5(g) at constant volume : 2N2O5(g)→2N2O4(g)+O2(g)
S. No.Time/sTotal pressure (atm)100.521000.512
Calculate the rate constant.View SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume.
2N2O5(g)→2N2O2(g)+O2(g)

Calculate the rate constant for the gaseous reaction.View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
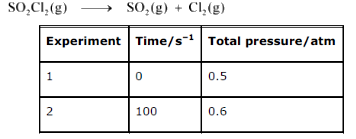
Calculate the rate of the reaction when total pressure is 0.65 atmView SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate of the reaction when total pressure is 0.65 atmView SolutionThe following data were obtained during the first order thermal decomposition of SO2CI2 at a constant volume.
SO2CI2(g)→SO2(g)+CI2(g)
ExperimentTime/s−1Total pressure/atm100.521000.6
What is the rate of reaction when total pressure is 0.65 atm?View Solution

