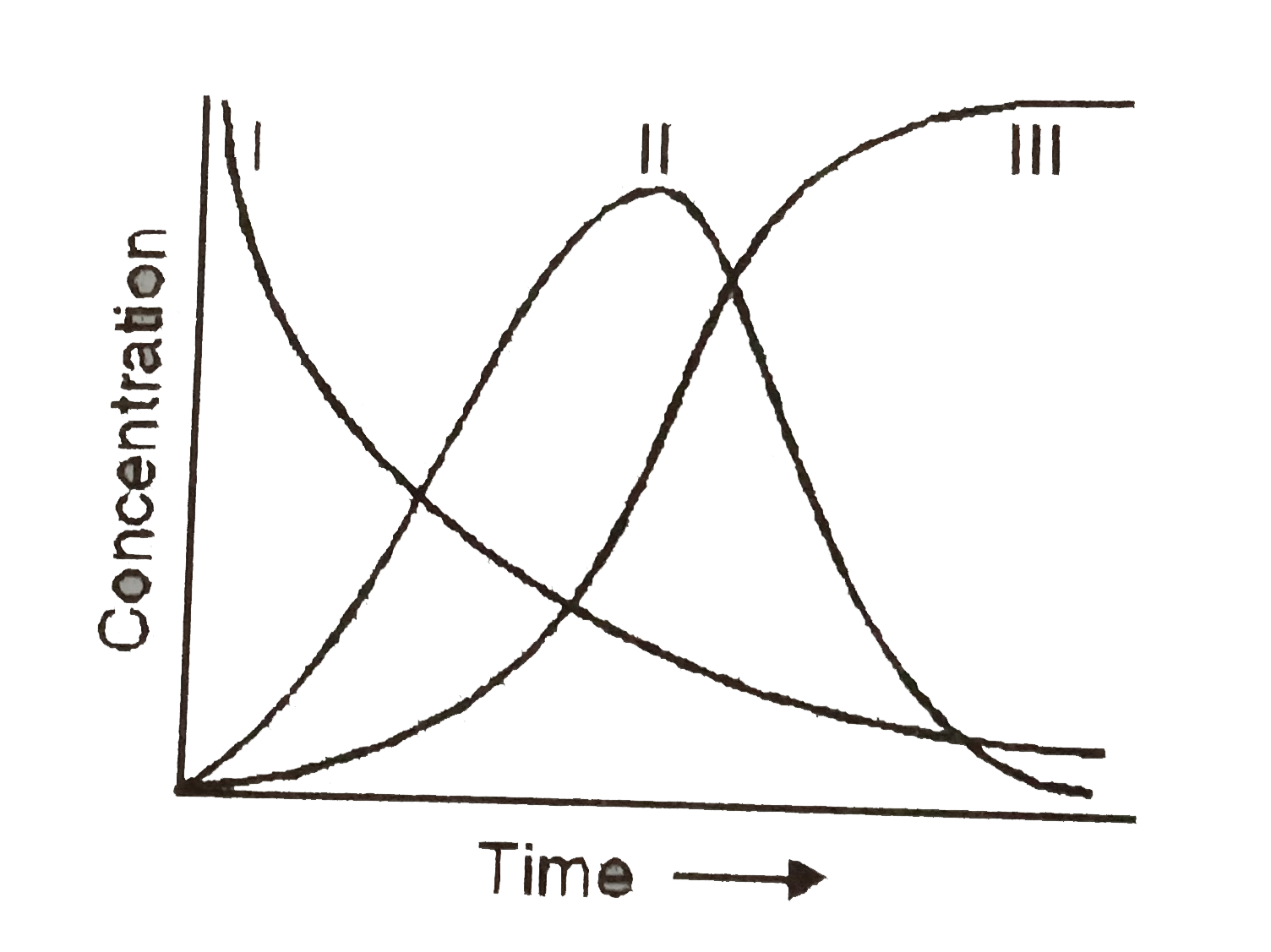
For a consecutive reaction $R_{1} k_{1} - - \to R_{2} k_{2} - - \to R_{3}$ , if initial concentration of $R_{1}$ is 100 M and $k_{1} : k_{2} = 1 : 0.15$ , calculate the value of $t_{max} (Given k_{1} = 4.0 \times 10^{- 2} {min}^{- 1}) .$

Video Solution

Text Solution

Verified by Experts

$t_{max}$ represents time corresponding to maximum concentration of the intermediate $R_{2}$
The value of $t_{max}$ is given by the relation
$t_{max} = \frac{2.303}{(k_{1} - k_{2})} log \frac{k_{1}}{k_{2}}$
$k_{1} = 4.0 \times 10^{- 2}$
$∴ k_{2} = 4.0 \times 10^{- 2} \times 0.15 = 6 \times 10^{- 3}$
$∴ t_{max} = \frac{2.303}{(4 - 0.6) 10^{- 2}} log \frac{4 \times 10^{- 2}}{6 \times 10^{- 3}} = \frac{2.303}{3.4 \times 10^{- 2}} \times 0.82 = 55.6 min$

|

Updated on:21/07/2023

Class 12 CHEMISTRY CHEMICAL KINETICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A consecutive reaction, $A K_{1} - - \to B K_{2} - - \to C$ is characterised by:
AMaximum in the concentration of $A$
BMaximum in the concentration of $B$
CMaximum in the concentration of $C$
DHighly exothermicity
Question 2 - Select One
For the consecutive unimolecular first order reaction $A k_{1} - - \to R k_{2} - - \to S$ , the concentration of component $A$ , $C_{A}$ at any time $t$ is given by
A $C_{=} C_{A_{0}} e^{(k_{1} + k_{2}) t}$
B $C_{A} = C_{A_{0}} e^{- (k_{1} + k_{2}) t}$
C $C_{A} = C_{A_{0}} e_{1}^{- k_{1} t}$
D $C_{A} = C_{A_{0}} e_{1}^{k_{1} t}$
Question 3 - Select One or More
For a reversible reaction $A k_{1} = 4 \times 10^{2} s^{- 1} \Leftarrow ====== \Rightarrow k_{2} = 2 \times 10^{2} s^{- 1} B$ initial concentration of A is 21 mol $L^{- 1}$ . Select the correct statement:
AEquilibrium concentration of A is 14 mol $L^{- 1}$
BEquilibrium conentration of B is 14 mol $L^{- 1}$ .
CThe concentration of A reduce by 50% of equilibrium concentration after 11.55 sec .
DThe concentration of A reduce to 50% after 23.1 sec.

PRADEEP-CHEMICAL KINETICS-HIGHER ORDER THINKING SKILLS (QUESTIONS AND PROBLEMS WITH ANSWERS/SOLUTIONS) HOTS PROBLEMS

Home
Ask Doubt
Profile