Question

Determine
the height of a mountain if the elevation of its top at an unknown distance
from the base is $30o$
and at a
distance 10km further off from the mountain, along the same line, the angle
of elevation is $15o$
. (Use $\tan 15o=0.27$
)

Explanation

To determine the height of the mountain based on the given angles of elevation, we can follow these steps:

1. Define the Variables:
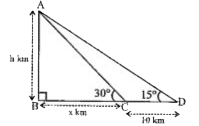
- Let the height of the mountain be \( h \).
- Let the distance from the base of the mountain to the point where the angle of elevation is \( 30^\circ \) be \( x \).
- The distance from this point to the second observation point (where the angle of elevation is \( 15^\circ \)) is \( 10 \) km.

2. Set Up the Right Triangle for \( 30^\circ \):
- From the first observation point (at distance \( x \)), we can use the tangent function:
\( \tan(30^\circ) = \frac{h}{x} \)
- We know that \( \tan(30^\circ) = \frac{1}{\sqrt{3}} \), so we can write:
\( \frac{1}{\sqrt{3}} = \frac{h}{x} \implies h = \frac{x}{\sqrt{3}} \tag{1} \)

3. Set Up the Right Triangle for \( 15^\circ \):
- From the second observation point (at distance \( x + 10 \)), we can use the tangent function again:
\( \tan(15^\circ) = \frac{h}{x + 10} \)
- Given that \( \tan(15^\circ) = 0.27 \), we can write:
\( 0.27 = \frac{h}{x + 10} \implies h = 0.27(x + 10) \tag{2} \)

4. Equate the Two Expressions for \( h \):
- From equations (1) and (2):
\( \frac{x}{\sqrt{3}} = 0.27(x + 10) \)

5. Solve for \( x \):
- Multiply both sides by \( \sqrt{3} \):
\( x = 0.27\sqrt{3}(x + 10) \)
- Distributing the right side:
\( x = 0.27\sqrt{3}x + 2.7\sqrt{3} \)
- Rearranging gives:
\( x - 0.27\sqrt{3}x = 2.7\sqrt{3} \)
- Factor out \( x \):
\( x(1 - 0.27\sqrt{3}) = 2.7\sqrt{3} \)
- Thus,
\( x = \frac{2.7\sqrt{3}}{1 - 0.27\sqrt{3}} \tag{3} \)

6. Substitute \( x \) Back to Find \( h \):
- Substitute equation (3) into equation (1):
\( h = \frac{x}{\sqrt{3}} = \frac{2.7\sqrt{3}}{\sqrt{3}(1 - 0.27\sqrt{3})} = \frac{2.7}{1 - 0.27\sqrt{3}} \)

7. Calculate \( h \):
- Calculate \( 0.27\sqrt{3} \) (approximately \( 0.27 \times 1.732 = 0.46764 \)):
\( 1 - 0.27\sqrt{3} \approx 1 - 0.46764 = 0.53236 \)
- Now calculate \( h \):
\( h \approx \frac{2.7}{0.53236} \approx 5.07 \text{ km} \)

Final Answer:
The height of the mountain is approximately \( 5.07 \) km.