If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length of 4.5 m on the ground, then the height of the lamp-post is
(a) 1.5 m (b) 2 m (c) 2.5 m (d) 2.8 m
To find the height of the lamp-post using the information given, we can use the concept of similar triangles. Here’s a step-by-step solution:
Step 1: Understand the scenario
We have a girl who is 1.5 m tall standing 3 m away from a lamp-post. She casts a shadow of 4.5 m. We need to find the height of the lamp-post.
Hint: Visualize the scenario by drawing a diagram showing the girl, her shadow, and the lamp-post.
Step 2: Identify the triangles
The situation creates two similar triangles:
1. Triangle formed by the girl and her shadow.
2. Triangle formed by the lamp-post and the combined length of the shadow and the distance from the girl to the lamp-post.
Hint: Remember that similar triangles have proportional sides.
Step 3: Set up the proportions
Let H be the height of the lamp-post. The lengths of the sides of the triangles give us the following proportions:
- For the girl:
Height of girlLength of shadow=1.54.5
- For the lamp-post:
Height of lamp-postTotal length from lamp-post to end of shadow=H4.5+3
which simplifies to:
H7.5
Hint: Write down the ratio of the heights to the lengths of the shadows for both triangles.
Step 4: Set the equations equal
Since the triangles are similar, we can set the ratios equal to each other:
1.54.5=H7.5
Hint: Cross-multiply to eliminate the fractions.
Step 5: Solve for H
Cross-multiplying gives:
1.5×7.5=H×4.5
Calculating the left side:
11.25=H×4.5
Now, divide both sides by 4.5 to solve for H:
H=11.254.5=2.5
Hint: Make sure to perform the division carefully to find the height.
Conclusion
The height of the lamp-post is H=2.5 meters.
Final Answer: (c) 2.5 m
We have a girl who is 1.5 m tall standing 3 m away from a lamp-post. She casts a shadow of 4.5 m. We need to find the height of the lamp-post.
The situation creates two similar triangles:
1. Triangle formed by the girl and her shadow.
2. Triangle formed by the lamp-post and the combined length of the shadow and the distance from the girl to the lamp-post.
Let H be the height of the lamp-post. The lengths of the sides of the triangles give us the following proportions:
- For the girl:
Height of girlLength of shadow=1.54.5
- For the lamp-post:
Height of lamp-postTotal length from lamp-post to end of shadow=H4.5+3
which simplifies to:
H7.5
Since the triangles are similar, we can set the ratios equal to each other:
1.54.5=H7.5
Cross-multiplying gives:
1.5×7.5=H×4.5
Calculating the left side:
11.25=H×4.5
Now, divide both sides by 4.5 to solve for H:
H=11.254.5=2.5
The height of the lamp-post is H=2.5 meters.
Topper's Solved these Questions
Similar Questions
A 1.6 m tall girl stands at distance of 3.2 m from a lamp post and casts shadow of 4.8 m on the ground, then what is the height of the lamp post?
View SolutionA 1.6m tall girl stands at a distance of 3.2m from a lamp-post and casts a shadow of 4.8m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
View Solution
Knowledge Check
If a 1.5 m-tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5m on the ground, then the height of the lamp-post is
A1.5mB2mC2.5mD2.8mA vertical pole 6 m log casts a shadow of length 3.6 m on the ground. What is the height of tower which casts a shadow of length 18 m at the same time?
A10.8mB28.8mC32.4mD30mvertical pole of length 3 m casts a shadow of 7 m and a tower casts a shadow of 28 m at a time. The height of tower is
A10 mB12 mC14 mD16 m
A boy 1.5 m tall standing from a lamp at a distance of 3m. The lamp casts a shadow of 4.5 m. Find the height of the lamp.
View SolutionA tree 6 m tall casts a shadow of length 4 m.At the same time a flag casts a shadow of length 50 m.Find the length of the pole
View Solution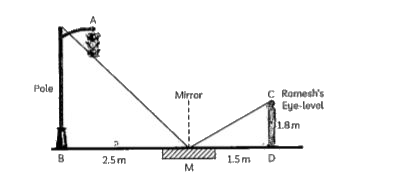
If the distance of Ramesh and the pole from the mirror are 2.5 m and 1.5 m respectively, then the height of the pole is:
View SolutionA vertical stick 20 m long casts a shadow 10m long on the ground. At the same time, a tower casts a shadow 50m long on the ground. The height of the tower is (a) 100m (b) 120m (c) 25m (d) 200m
View SolutionA pole of height 6 m casts a shadow 2√3 m long on the ground. Find the sun's elevation.
View Solution
