A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. 15.16. Find: (i) the total length of the silver wire required (ii) the area of each sector of the brooch.
To solve the problem step by step, we will break it down into two parts as required:
Part (i): Total Length of the Silver Wire Required
1. Calculate the Circumference of the Circle:
- The formula for the circumference C of a circle is given by:
C=π×d
- Here, the diameter d is 35 mm.
- Substituting the value:
C=π×35 mm≈3.14×35≈109.9 mm
2. Calculate the Length of the Diameters:
- The problem states that there are 5 diameters used to divide the circle into 10 equal sectors.
- The length of one diameter is equal to the diameter of the circle, which is 35 mm.
- Therefore, the total length of the 5 diameters is:
Total length of diameters=5×35 mm=175 mm
3. Calculate the Total Length of the Silver Wire:
- The total length of the silver wire required is the sum of the circumference of the circle and the total length of the diameters:
Total length=C+Total length of diameters=109.9 mm+175 mm=284.9 mm
Part (ii): Area of Each Sector of the Brooch
1. Calculate the Area of the Circle:
- The formula for the area A of a circle is given by:
A=πr2
- First, we need to find the radius r:
r=d2=35 mm2=17.5 mm
- Now, substituting the radius into the area formula:
A=π×(17.5 mm)2≈3.14×306.25≈962.5 mm2
2. Calculate the Area of Each Sector:
- Since the circle is divided into 10 equal sectors, the area of each sector is:
Area of each sector=A10=962.5 mm210≈96.25 mm2
Final Answers:
(i) The total length of the silver wire required is approximately 284.9 mm.
(ii) The area of each sector of the brooch is approximately 96.25 mm².
- The formula for the circumference C of a circle is given by:
C=π×d
- Here, the diameter d is 35 mm.
- Substituting the value:
C=π×35 mm≈3.14×35≈109.9 mm
- The problem states that there are 5 diameters used to divide the circle into 10 equal sectors.
- The length of one diameter is equal to the diameter of the circle, which is 35 mm.
- Therefore, the total length of the 5 diameters is:
Total length of diameters=5×35 mm=175 mm
- The total length of the silver wire required is the sum of the circumference of the circle and the total length of the diameters:
Total length=C+Total length of diameters=109.9 mm+175 mm=284.9 mm
- The formula for the area A of a circle is given by:
A=πr2
- First, we need to find the radius r:
r=d2=35 mm2=17.5 mm
- Now, substituting the radius into the area formula:
A=π×(17.5 mm)2≈3.14×306.25≈962.5 mm2
- Since the circle is divided into 10 equal sectors, the area of each sector is:
Area of each sector=A10=962.5 mm210≈96.25 mm2
(i) The total length of the silver wire required is approximately 284.9 mm.
(ii) The area of each sector of the brooch is approximately 96.25 mm².
Topper's Solved these Questions
Similar Questions
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in the given figure. Find

The total length of the silver wire required.
(Use π=227 )
View SolutionA brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors. Find :
(i) the total length of the silver wire required.
(ii) the area of each sector of the brooch.
View SolutionA brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in the given figure. Find

The area of each sector of the brooch.
(Use π=227 )
View SolutionA brooch is a small piece of jewellery which has a pin at the back so it can be fastened on a dress, blouse or coat.Designs of some brooch are shown below. Observe them carefully.
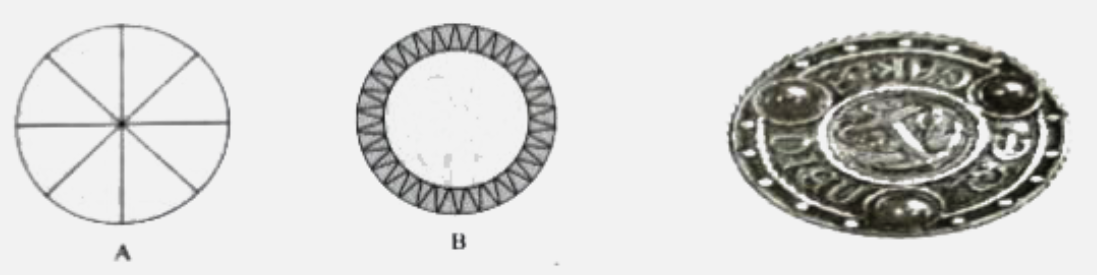
Design A: Brooch A is made with silver wire in the form of a circle with diameter 28mm. The wire used for making 4 diameters which divide the circle into 8 equal parts.
Design B: Brooch b is made two colours_ Gold and silver. Outer part is made with Gold. The circumference of silver part is 44mm and the gold part is 3mm wide everywhere.
Refer to Design A
The area of each sector of the brooch is
View SolutionA brooch is a small piece of jewellery which has a pin at the back so it can be fastened on a dress, blouse or coat.Designs of some brooch are shown below. Observe them carefully.

Design A: Brooch A is made with silver wire in the form of a circle with diameter 28mm. The wire used for making 4 diameters which divide the circle into 8 equal parts.
Design B: Brooch b is made two colours_ Gold and silver. Outer part is made with Gold. The circumference of silver part is 44mm and the gold part is 3mm wide everywhere.
Refer to Design A
The total length of silver wire required is
View SolutionA brooch is a small piece of jewellery which has a pin at the back so it can be fastened on a dress, blouse or coat.Designs of some brooch are shown below. Observe them carefully.

Design A: Brooch A is made with silver wire in the form of a circle with diameter 28mm. The wire used for making 4 diameters which divide the circle into 8 equal parts.
Design B: Brooch b is made two colours_ Gold and silver. Outer part is made with Gold. The circumference of silver part is 44mm and the gold part is 3mm wide everywhere.
Refer to Design B
The difference of areas of golden and silver parts is
View SolutionA brooch is a small piece of jewellery which has a pin at the back so it can be fastened on a dress, blouse or coat.Designs of some brooch are shown below. Observe them carefully.

Design A: Brooch A is made with silver wire in the form of a circle with diameter 28mm. The wire used for making 4 diameters which divide the circle into 8 equal parts.
Design B: Brooch b is made two colours_ Gold and silver. Outer part is made with Gold. The circumference of silver part is 44mm and the gold part is 3mm wide everywhere.
Refer to Design B
The circumference of outer part (golden) is
View SolutionA brooch is a small piece of jewellery which has a pin at the back so it can be fastened on a dress, blouse or coat.Designs of some brooch are shown below. Observe them carefully.

Design A: Brooch A is made with silver wire in the form of a circle with diameter 28mm. The wire used for making 4 diameters which divide the circle into 8 equal parts.
Design B: Brooch b is made two colours_ Gold and silver. Outer part is made with Gold. The circumference of silver part is 44mm and the gold part is 3mm wide everywhere.
Refer to Design B
A boy is playing with brooch B. He makes revolution with it along its edge. How many complete revolutions must it take to cover 80π mm ?
View SolutionIn a circle of radius 6 cm, a chord of length 10 cm makes an angle of 110o at the centre of the circle. Find (i) the length of the arc AB , (ii) the area of the sector OAB .
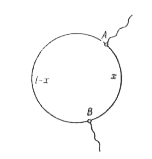
View SolutionA circular ring made of copper wire of 0.1 mm diameter and 60 cm long is connected as shown in Fig. 26.1. Find the resistance of the circuit. What should the length of the shorter section AB = x be for the resistance of the circuit to be 0.2 ohm?
View Solution
