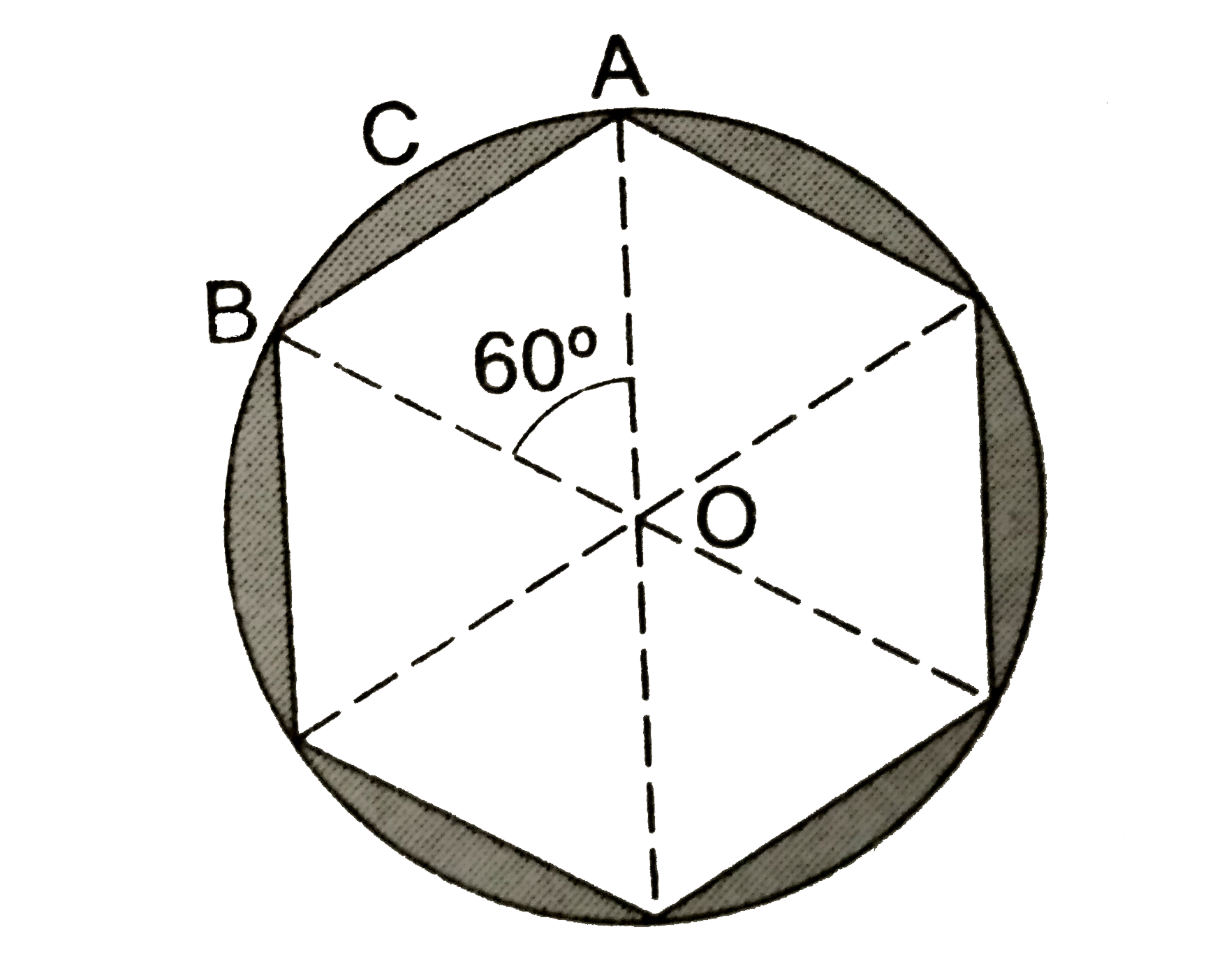
A round table cover has six equal designs as shown in Fig. 15.51. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs 3.50 per cm2 . (Use √3=1.7) (FIGURE)
To solve the problem of finding the cost of making the designs on a round table cover with a radius of 28 cm, we will follow these steps:
Step 1: Calculate the area of one design
Since there are 6 equal designs on the round table cover, we first need to determine the area of one design. Each design corresponds to a sector of the circle with a central angle of 60∘ (since 360∘/6=60∘).
The formula for the area of a sector is given by:
Area=θ360×πr2
where θ is the angle in degrees and r is the radius.
Substituting the values:
- θ=60∘
- r=28cm
- π≈227
The area of one design is:
Area=60360×227×(28)2
Step 2: Simplify the area calculation
Calculating the area step-by-step:
1. Calculate (28)2=784.
2. Now substitute this back into the area formula:
Area=16×227×784
Step 3: Calculate the total area of all designs
Since there are 6 designs, the total area A is:
A=6×Area of one design
Step 4: Calculate the cost
The cost of making the designs is given by:
Cost=Area×Rate
where the rate is Rs 3.50 per cm².
Step 5: Substitute and calculate
Now, substituting the values:
1. Calculate the area of one design:
Area of one design=16×227×784=22×78442=1724842≈410.67cm2
2. Total area for 6 designs:
A=6×410.67≈2464.02cm2
3. Finally, calculate the cost:
Cost=2464.02×3.50≈8614.07
Final Answer
The total cost of making the designs is approximately Rs 8614.07.
Since there are 6 equal designs on the round table cover, we first need to determine the area of one design. Each design corresponds to a sector of the circle with a central angle of 60∘ (since 360∘/6=60∘).
Area=θ360×πr2
where θ is the angle in degrees and r is the radius.
- θ=60∘
- r=28cm
- π≈227
Area=60360×227×(28)2
Calculating the area step-by-step:
1. Calculate (28)2=784.
2. Now substitute this back into the area formula:
Area=16×227×784
Since there are 6 designs, the total area A is:
A=6×Area of one design
The cost of making the designs is given by:
Cost=Area×Rate
where the rate is Rs 3.50 per cm².
Now, substituting the values:
1. Calculate the area of one design:
Area of one design=16×227×784=22×78442=1724842≈410.67cm2
2. Total area for 6 designs:
A=6×410.67≈2464.02cm2
3. Finally, calculate the cost:
Cost=2464.02×3.50≈8614.07
The total cost of making the designs is approximately Rs 8614.07.
Topper's Solved these Questions
Similar Questions
A round table cover has six equal designs as shown in Fig. 12.14. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs 0.35 per cm2.
 View Solution
View SolutionA round table cover has six equal designs as shown in Fig. 15.51. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs 3.50 per cm2 . (Use √3=1.7) (FIGURE)
View SolutionA round table cover has six and equal designs, as shown in the figure. If the radius of the cover is 28 cm find the cost of making the designs, at the rate of Rs. 0.35 per cm2. [ Use √3=1.7]
 View Solution
View SolutionCombination of polygon and Circle : A round table cover has 6 equal designs as shown in figure. If the radius of the cover is 28cm find the cost of making the designs at the rate of Rs. 0.35 per cm2
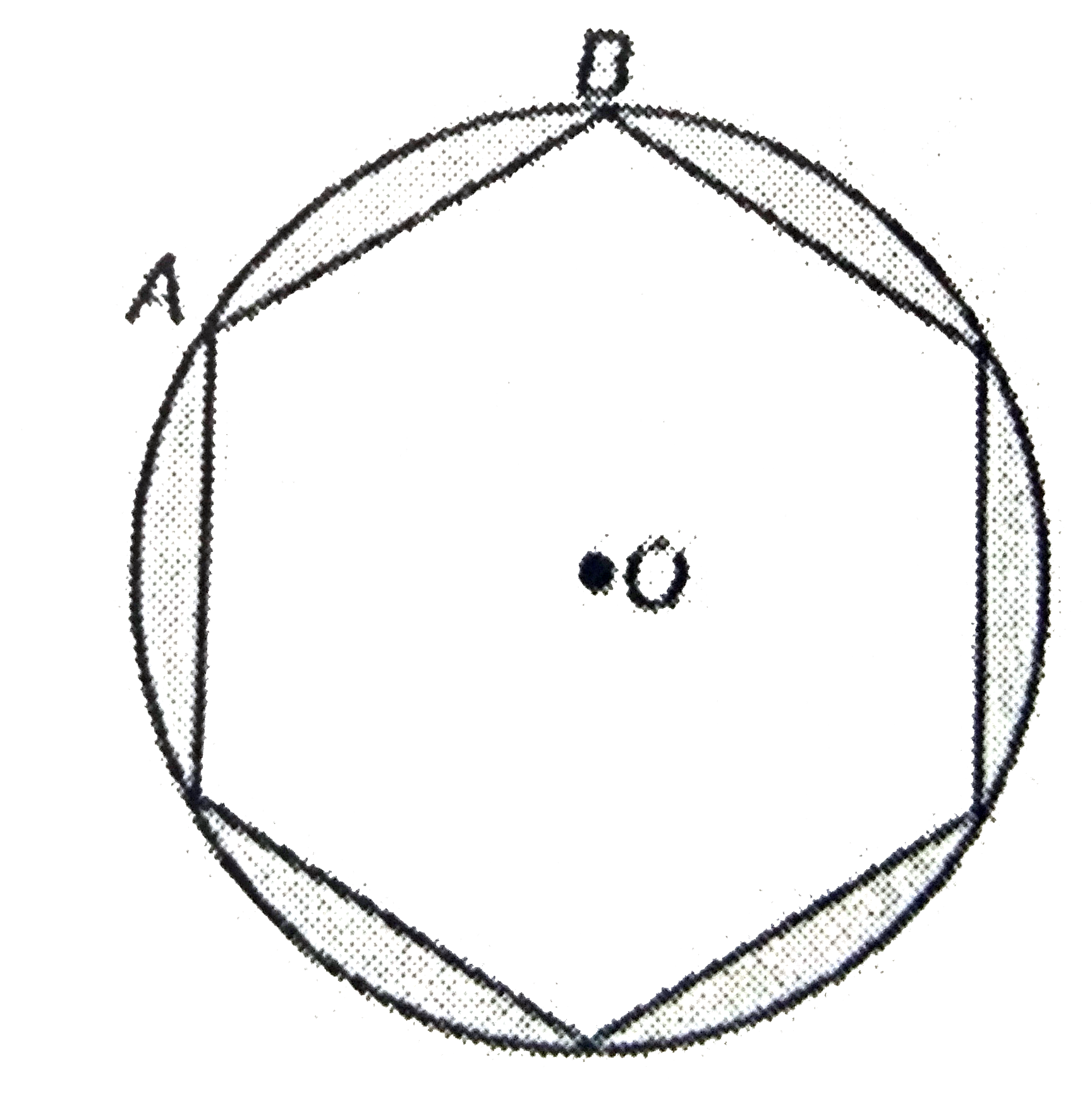
View SolutionA round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm then find the total area of the design. (Use √3=1.732andπ=3.14)
 View Solution
View SolutionA round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm then find the total area of the design. [Use √3=1.732 and π=3.14]
 View Solution
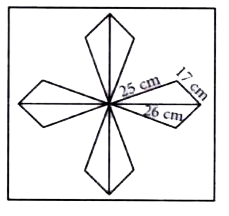
View SolutionA design is madeon a rectangular tile as shown in the given figure. The design has eight triangles, each of the side 25 cm, 17 cm and 26 cm. Find the total cost of making the design at the rate of 3.50 per cm2.
 View Solution
View SolutionIn a temple there are 25 cylindrical pillars. The radius of each pillar is 28cm and height 4m. Find the total cost of painting the curved surface area of pillars at the rate of Rs. 8perm2
View SolutionA solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each of the hemispherical ends is 7 cm, find the cost of polishing its surface at the rate of Rs 10 per dm2
View SolutionA bucket has top and bottom diameters of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs 1.20 per cm2 .
View Solution

