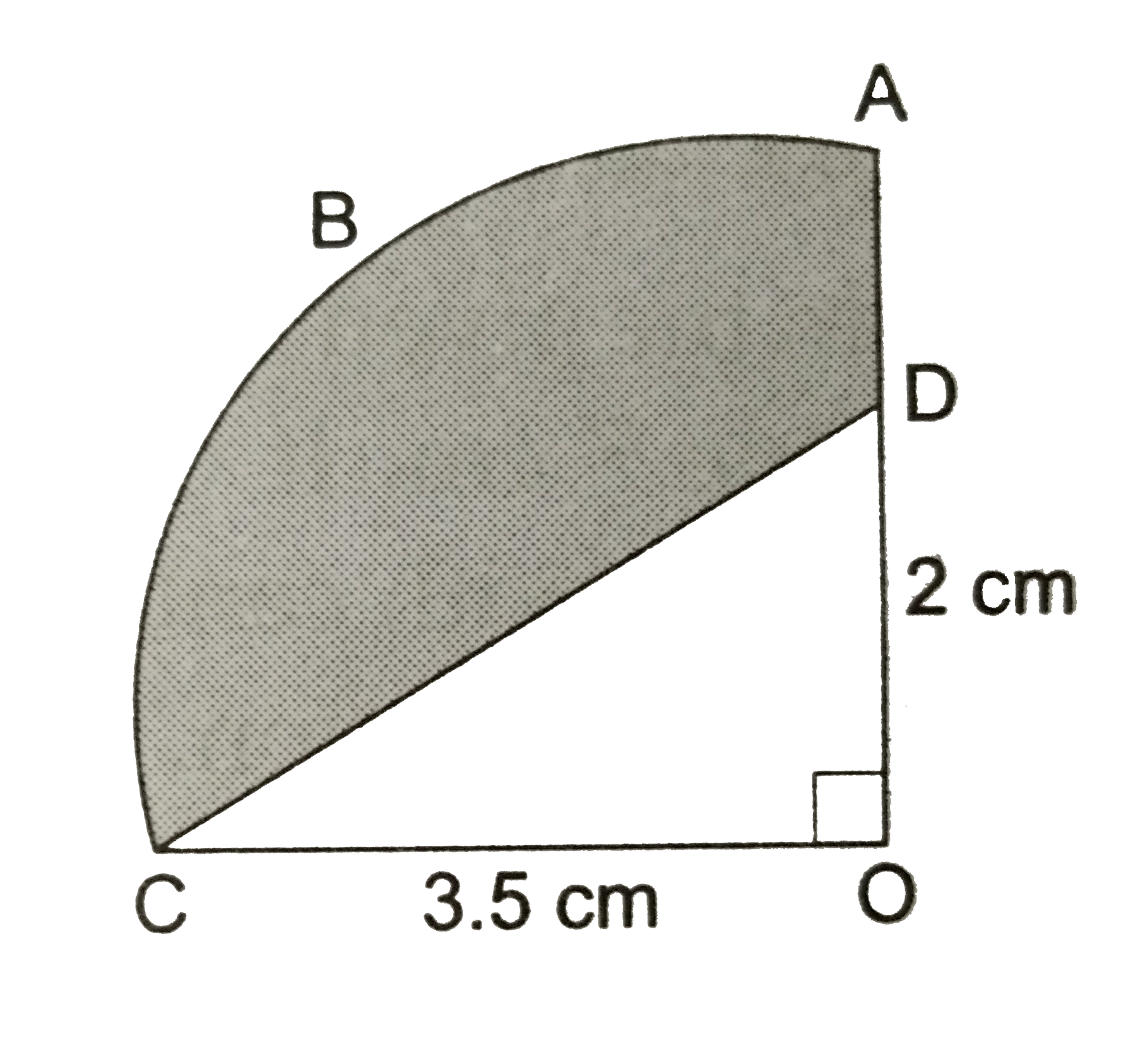
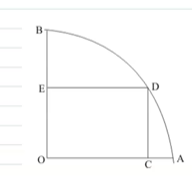
In Fig. 15.70, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2 cm , find the area of the (i) quadrant OACB (ii) shaded region. (FIGURE)
Step by step video & image solution for In Fig. 15.70, O A C B is a quadrant of a circle with centre O and radius 3.5 cm. If O D=2\ c m , find the area of the (i) quadrant O A C B (ii) shaded region. (FIGURE) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Fig. 12.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2cm, find the area of the
(i) quadrant OACB, (ii) shaded region.
View SolutionIn the given figwe, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.
View SolutionIn figure, OACB is a quadrant of a circle with centre O and radius 7 cm. If AD = 2 cm, find the area of the shaded region.
View SolutionOACB is a quadrant of a circle with centre O and its radius is 3.5cm . If OD=2cm, find the area of the shaded region. [Take π=227]

View SolutionIn the given figure OABC is a quadrant of a circle with centre O and radius 3.5cm.If OD=2cm,find the area of the shaded region.
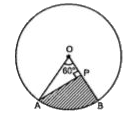
View SolutionIn the given figure, AOB is a sector of angle 60∘ of a circle with centre O and radius 17 cm. If AP ⊥ OB and AP = 15 cm, find the area of the shaded region.
View SolutionIn Fig. 15.99, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA=21 cm , find the area of the shaded region. (FIGURE)
View SolutionIn Figure, OCDE is a rectangle inscribed in a quadrant of a circle of radius 10cm. If OE=2√5 , find the area of the rectangle.
View SolutionIn Fig. 15.92, two circles with centres A and B touch each other at the point C . If AC=8 cm and AB=3 cm , find the area of the shaded region. (FIGURE)
View SolutionIn Fig. 15.69, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA=7 cm , find the area of the shaded region. (FIGURE)
View Solution
