A triangle ABC is an isosceles triangle if any one of the following conditions hold: Bisector of ∠BAC is perpendicular to the base BC
In △ADBandADC
∠BAD=∠CAD
AD is bisector of ∠BAC
AD=AD
△ADB=△ADC (Each equal to 90^0)
△ADB≅/_\ ADC (By ASA congruence Criterion
AB=AC(CPCT)
Hence, triangle ABC is isosceles.
Topper's Solved these Questions
Similar Questions
A triangle ABC is an isosceles triangle if any one of the following conditions hold: Bisector of ∠BAC is perpendicular to the base BC
View SolutionA triangle ABC is an isosceles triangle if any one of the following conditions hold: Altitude AD bisects ∠BAC Bisector of ∠BAC is perpendicular to the base BC
In triangle,ABC
let the altitude AD bisects ∠BAC
Then we have to prove that the triangle ABC, is isosceles.
In △s ADB and ADC,<br>/_BAD=/_CAD<br>(ADisbisec→rof/_BAC)<br>AD=AD(common)<br>/_ADB=/_ADC(Eachequal→90)<br>=>/_\ADB~=/_\ADC(byASA≅ruencecriterion)<br>AB=AC(cpct)<br>Hence,A△A B C is an isoscelesView Solution
Knowledge Check
- Question 1 - Select One or More
If a,b,c are the sides of a triangle then which of the following hold good?
Aa2+b2+c2>ab+bc+caBa2+b2+c2ab+bc+ca lies between 1 and 2Ca3+b3+c3>3abcD3(ab+bc+ca)≤(a+b+c)2≤4(bc+ca+ab) - Question 2 - Select One
ABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(-2,7), the coordinates of vertex A can be
A(1,6)B(−1/2,5)C(−5/6,6)Dnone of these - Question 3 - Select One or More
ABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(-2,7), the coordinates of vertex A can be
A(1,6)B(−12,5)C(56,6)D(−7,18)
A triangle ABC is an isosceles triangle if any one of the following conditions hold: Altitude AD bisects ∠BAC. Bisector of ∠BAC is perpendicular to the base BC.
View SolutionIf the median to the base of a triangle is perpendicular to the base then triangle is isosceles.
View SolutionIf the median to the base of a triangle is perpendicular to the base, then triangle is isosceles.
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
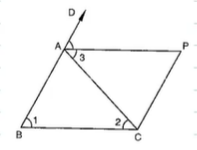 View Solution
View SolutionIn any triangle ABC , prove that following: bcosB+c cos C=acos(B−C)
View Solution

