Two parallel side of a
trapezium are 60cm and 77cm
and other sides are 25cm and 26cm.
Find the area of the
trapezium.
To find the area of the trapezium with parallel sides of lengths 60 cm and 77 cm, and non-parallel sides of lengths 25 cm and 26 cm, we can follow these steps:
Step 1: Identify the lengths of the sides
Let the lengths of the parallel sides be:
- a=60cm (one parallel side)
- b=77cm (other parallel side)
And the lengths of the non-parallel sides be:
- c=25cm
- d=26cm
Step 2: Calculate the semi-perimeter of the trapezium
The semi-perimeter s of the trapezium can be calculated using the formula:
s=a+b+c+d2
Substituting the values:
s=60+77+25+262=1882=94cm
Step 3: Calculate the area of the trapezium using Heron's formula
To find the area A of the trapezium, we can divide it into two triangles by drawing a height from one of the non-parallel sides to the longer parallel side. We will find the area of the triangles using Heron's formula.
1. Triangle 1 (with sides a,c,h):
- a=60cm
- c=25cm
- h is the height we need to find.
2. Triangle 2 (with sides b,d,h):
- b=77cm
- d=26cm
Step 4: Calculate the area of each triangle
Using Heron's formula for each triangle, we first need to calculate the semi-perimeter for each triangle.
For Triangle 1:
s1=60+25+h2
Area A1 is given by:
A1=√s1(s1−60)(s1−25)(s1−h)
For Triangle 2:
s2=77+26+h2
Area A2 is given by:
A2=√s2(s2−77)(s2−26)(s2−h)
Step 5: Combine the areas to find the total area of the trapezium
The total area A of the trapezium is:
A=A1+A2
Step 6: Calculate the height of the trapezium
To find the height h, we can use the formula for the area of a trapezium:
A=12×(a+b)×h
Substituting the values we have:
A=12×(60+77)×h
Step 7: Solve for h
Rearranging gives:
h=2A(60+77)
Step 8: Final area calculation
Now we can calculate the area using the trapezium area formula:
A=12×(60+77)×h
Let the lengths of the parallel sides be:
- a=60cm (one parallel side)
- b=77cm (other parallel side)
- c=25cm
- d=26cm
The semi-perimeter s of the trapezium can be calculated using the formula:
s=a+b+c+d2
Substituting the values:
s=60+77+25+262=1882=94cm
To find the area A of the trapezium, we can divide it into two triangles by drawing a height from one of the non-parallel sides to the longer parallel side. We will find the area of the triangles using Heron's formula.
- a=60cm
- c=25cm
- h is the height we need to find.
- b=77cm
- d=26cm
Using Heron's formula for each triangle, we first need to calculate the semi-perimeter for each triangle.
s1=60+25+h2
Area A1 is given by:
A1=√s1(s1−60)(s1−25)(s1−h)
s2=77+26+h2
Area A2 is given by:
A2=√s2(s2−77)(s2−26)(s2−h)
The total area A of the trapezium is:
A=A1+A2
To find the height h, we can use the formula for the area of a trapezium:
A=12×(a+b)×h
Substituting the values we have:
A=12×(60+77)×h
Rearranging gives:
h=2A(60+77)
Now we can calculate the area using the trapezium area formula:
A=12×(60+77)×h
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The parallel sides of a trapezium are 20 m and 30 m and its non-parallel sides are 6 m and 8 m. Find the area of the trapezium.
A96 m2B82 m2C100 m2D120 m2 - Question 2 - Select One
The parallel sides of a trapezium field are 12 m and 20 m. If distance between the parallel sides is 8 m, find the area of the field.
A128 sqmB132 sq mC130 sq mD135 sq m - Question 3 - Select One
The length of the parallel sides of a trapezium are 51 cm and 21 cm , and that of each of the other two sides is 39 cm. What is the area ( in cm2 ) of the trapezium ?
A1360B1296C1152D1206
The parallel sides of a trapezium are 25cm and 5cm and 13cm. Find the area of the trapezium
View SolutionThe parallel sides of a trapezium are 25cm and 13cm; its nonparallel sides are equal, each being 10cm, find the area of the trapezium.
View SolutionIn Figure, ABCD is a rectangle with sides AB=10cmandAD=5cm Find the area of EFG
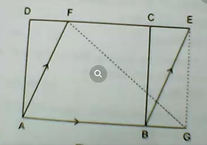 View Solution
View SolutionFind the area of a trapezium whose parallel sides 25cm,13cm and other sides are 15cmand15cm.
View SolutionThe parallel sides of a field in the shape of a trapezium are 20 m and 41 m and the reamaining two sides are 10 m and 17 m. Find the cost of levelling the field at the rate of 30 per square meter ?
View Solution

