If PQRS is a square, then write the measure of ∠SRP
given that PQRS is a square,
consider a traingle PSR
PS=RS[sides of a square]
so it is a isosceles triangle.
∠SRP=∠RPS
let ∠SRP=∠RPS=x∘
∠PSR=90∘ [angle of a square]
so
∠PSR+∠SRP+∠RPS=180∘
2x=180∘−90∘
x=45∘
hence ∠SRP=45∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If the sum of the square of p and twice of q is equal to the square root of the sum of the square of r and s, wirte a formula wth p as the subject.
Ap=√2p−√r2+s2Bp=√r2+s2−2qCp=√2q−r2−s2Dp=√1−k2 - Question 2 - Select One
If the sum of the square of p and twice of q is equal to the square root of the sum of the square of r and s, wirte a formula wth p as the subject.
Ap=√2q−√r2+s2Bp=√r2+s2−2qCp=√2q−r2−s2Dp=√1−k2 - Question 3 - Select One
Let a:~(p∧~r)∨(~q∨s)andb:(p∨s)lar(q∧r). If the truth values of p and q are true and that of r and s are false, then the truth values of a and b are respectively . . .
AF,FBT,TCT,FDF,T
In Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
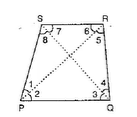 View Solution
View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionGIVEN : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. TO PROVE : (i) ∠R>∠P (ii) ∠S>∠Q CONSTRUCTION : Join PR and QS. Figure
View SolutionIn Fig. 6.43, if PQ⊥PS,PQ∣∣SR,∠SQR=28∘ and ∠QRT=65∘, then find the values of x and y.
 View Solution
View Solution


